
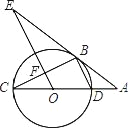
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.
(1)求证:△BEF∽△DBC.
(2)若⊙O的半径为3,∠C=30°,求BE的长.
【答案】(1)见解析;(2)BE=3![]() .
.
【解析】
(1)连接OB,根据切线的性质可得出∠ABO=90°,由OB=OD可得出∠OBD=∠ODB,根据等角的余角相等可得出∠EBF=∠CDB,根据平行线的性质结合直径对的圆周角为90度,即可得出∠EFB=∠CBD=90°,进而即可证出△BEF∽△DCB;
(2)通过解直角三角形可得出BD、BC的长,由三角形中位线定理可得出BF的长,再利用相似三角形的性质即可求出BE的长.
(1)证明:连接OB,如图所示.
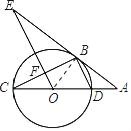
∵AE与⊙O相切,
∴∠ABO=90°.
∵OB=OD,
∴∠OBD=∠ODB.
∵∠ABO=∠ABD+∠OBD=90°,
∴∠ODB+∠ABD=90°.
∵CD为直径,
∴∠CBD=90°,
∴∠EBF+∠ABD=90°,
∴∠EBF=∠ODB,即∠EBF=∠CDB.
∵OE∥BD,
∴∠CFO=90°,
∴∠EFB=∠CBD=90°,
∴△BEF∽△DCB.
(2)解:在Rt△BCD中,∠CBD=90°,∠C=30°,CD=6,
∴BD=3,BC=3![]() .
.
∵OE∥BD,点O为CD的中点,
∴OF为△BCD的中位线,
∴OF=![]() BD=
BD=![]() ,BF=
,BF=![]() BC=
BC=![]() .
.
∵△BEF∽△DCB,
∴![]() ,即
,即![]() ,
,
∴BE=![]() .
.


科目:初中数学 来源: 题型:
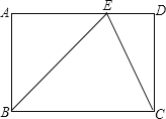
【题目】如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论;
(2)若AB=2,∠DCE=22.5°,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
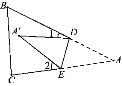
【题目】如图,把一张三角形纸片沿DE折叠,当点A落在四边形BCED的内部时,∠A、∠1、∠2之间的关系是( )
A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2
C. 3∠A=∠1+∠2 D. 4∠A=∠1+∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AB=4,则图中阴影部分的面积为_____(结果保留π).
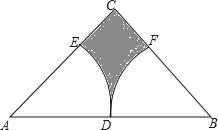
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.
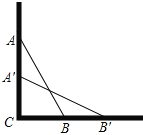
(1)这云梯的顶端距地面AC有多高?
(2)如果云梯的顶端A下滑了4米,那么它的底部B在水平方向向右滑动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是等边三角形,
是等边三角形,![]() 为平面内的一个动点,
为平面内的一个动点,![]() ,
,![]() 平分
平分![]() ,且
,且![]() .
.
(1)当![]() 与
与![]() 重合时(如图1),求
重合时(如图1),求![]() 的度数;
的度数;
(2)当![]() 在
在![]() 的内部时(如图2),求
的内部时(如图2),求![]() 的度数;
的度数;
(3)当![]() 在
在![]() 的外部时,请你直接写出
的外部时,请你直接写出![]() 的度数为 .
的度数为 .
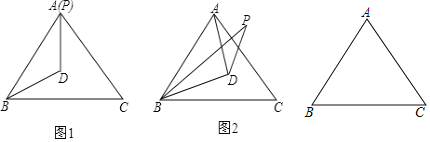
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示转盘平均分成![]() 份,分别标有
份,分别标有![]() ,
,![]() ,…,
,…,![]() 这
这![]() 个数字,转盘上有固定的指针,转动转盘,当转盘停止转动时,指针指向的区域对应的数字即为转出的数字(若指针指向分界处要重新转动,直至指到非分界处).
个数字,转盘上有固定的指针,转动转盘,当转盘停止转动时,指针指向的区域对应的数字即为转出的数字(若指针指向分界处要重新转动,直至指到非分界处).
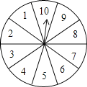
(1)转出的数字为奇数的概率是多少?
(2)转出的数字是![]() 的倍数的概率是多少?
的倍数的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com