
����Ŀ����ͼ��ij������ҵ�ֵ���ڣ���ѧ������ȤС���ͬѧ����������ѧ��֪ʶ��������֧�ܵ���ߵ�E������ľ���EF����������֧�ܵ�����BC����洹ֱ������BCA=90�㣬��BC=1.5m����F��A��C��ͬһ��ˮƽ���ϣ�б��AB��ˮƽ��AC�ļн���BAC=30�㣬֧�Ÿ�DE��AB�ڵ�D����֧�ܵı�BE��AB�ļн���EBD=60�㣬�ֲ��AD=1m�����������֧�ܵı�BE������E������ľ���EF�ij��ȣ�
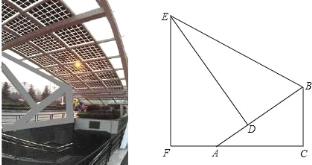
���𰸡���֧�ܵı�BEΪ4m������E������ľ���EF�ij���Ϊ3.5m��
��������
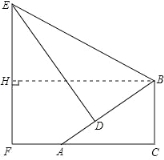
�����������B��BH��EF�ڵ�H����Rt��ABC�У�������BAC=30�㣬BC=1.5�������AB�ij��ȣ���AD=1m�������BD�ij��ȣ���Rt��EBD�н�ֱ�����������EB�ij��ȣ�Ȼ�����BH��EF�������EBH=30�㣬�̶������EH�ij��ȣ���EF=EH+HF��ֵ��
�����������B��BH��EF�ڵ�H��
���ı���BCFHΪ���Σ�BC=HF=1.5m����HBA=��BAC=30�㣬
��Rt��ABC�У��ߡ�BAC=30�㣬BC=1.5m����AB=3m����AD=1m����BD=2m��
��Rt��EDB�У��ߡ�EBD=60�㣬
���BED=90�㩁60��=30�㣬
��EB=2BD=2��2=4m��
���ߡ�HBA=��BAC=30�㣬
���EBH=��EBD����HBD=30�㣬
��EH=![]() EB=2m��
EB=2m��
��EF=EH+HF=2+1.5=3.5��m����
�𣺸�֧�ܵı�BEΪ4m������E������ľ���EF�ij���Ϊ3.5m��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����̣�m+2��x|m|+3mx+1��0 �ǹ��� x ��һԪ���η��̣��� m ��ֵΪ�� ��
A. ��2 B. +2 C. ��2 D. ���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼����DZ�Ȼ�¼��ǣ� ��
A������̫������������
B�������Ա�ڷ�����Ͷ��һ�Σ�δͶ��
C��ʵ������Ͷ��ˮ�л����ˮ��
D���׳�һöӲ�ң���غ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���㣨1��-2�����ڵ������ǣ� )
A.��һ����B.�ڶ�����C.��������D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB=BC=4������ABC��AC���۵õ���ADC����
��1���ı���ABCD�� �Σ�
��2������B=120������P��E��F�ֱ�Ϊ�߶�AC��AD��DC�ϵ�����1�㣬��PE+PF����СֵΪ ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com