
分析 根据正数,负数,非负整数,有理数的定义可得出答案.
解答 解:正数集合{15,0.81,$\frac{1}{4}$,171,3.14,π …}
负数集合{-$\frac{1}{2}$,-3,-3.1,-4…}
非负整数集合{15,171,0 …}
有理数集合{15,-$\frac{1}{2}$,0.81,-3,$\frac{1}{4}$,-3.1,-4,171,0,3.14…}.
故答案为:{15,0.81,$\frac{1}{4}$,171,3.14,π …};{-$\frac{1}{2}$,-3,-3.1,-4…};{15,171,0 …};{15,-$\frac{1}{2}$,0.81,-3,$\frac{1}{4}$,-3.1,-4,171,0,3.14…}.
点评 本题考查了有理数,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点,注意整数和正数的区别,注意0是整数,但不是正数.


科目:初中数学 来源: 题型:解答题
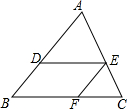 已知:如图,在△ABC中,DE∥BC,EF∥AB,$\frac{AD}{DB}$=$\frac{3}{2}$,BC=25,求:FC的长.
已知:如图,在△ABC中,DE∥BC,EF∥AB,$\frac{AD}{DB}$=$\frac{3}{2}$,BC=25,求:FC的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
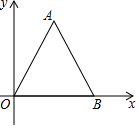 在平面直角坐标系中,等边△AOB的位置如图,若OB=3,则点A的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
在平面直角坐标系中,等边△AOB的位置如图,若OB=3,则点A的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
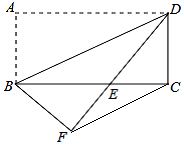 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.连结CF
如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.连结CF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线交x轴于A(-1,0),B(3,0),交y轴于C(0,-3),以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,交⊙M的切线AE于E,连接DM并延长交⊙M于N,连接AN,AD.
已知抛物线交x轴于A(-1,0),B(3,0),交y轴于C(0,-3),以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,交⊙M的切线AE于E,连接DM并延长交⊙M于N,连接AN,AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com