
 ��֪�����߽�x����A��-1��0����B��3��0������y����C��0��-3������ABΪֱ������M������������һ��P����M������PD���е�ΪD������M������AE��E������DM���ӳ�����M��N������AN��AD��
��֪�����߽�x����A��-1��0����B��3��0������y����C��0��-3������ABΪֱ������M������������һ��P����M������PD���е�ΪD������M������AE��E������DM���ӳ�����M��N������AN��AD������ ��1���������������ߵĺ�����ϵʽΪ��y=a��x+1����x-3������C��0��-3���������a�������䷽������������꼴�ɣ�
��2����֤����EAM�ա�EDM��HL��������Ϊ�ı���EAMD�����Ϊ4 $\sqrt{3}$���Ƴ�S��EAM=2 $\sqrt{3}$���Ƴ� $\frac{1}{2}$AM•AE=2 $\sqrt{3}$����AM=2���Ƴ�AE=2 $\sqrt{3}$���Ƴ���E������ΪE1��-1��2 $\sqrt{3}$����E2��-1��-2 $\sqrt{3}$�������������������������D�����꼴�����ô���ϵ����������⣮
��3��������S�ı���EAMD=2S��EAM��S��DAN=2S��AMD���Ƴ�S��AMD=S��EAM���Ƴ�E��D���㵽x��ľ�����ȣ���PD���M���У��Ƴ���D���E��x��ͬ�࣬�Ƴ�����PD��x��ƽ�У���ʱ����PD�ĺ�����ϵʽΪy=2��y=-2����y=2ʱ����y=x2-2x-3�ã�x=1��$\sqrt{6}$����y=-2ʱ����y=x2-2x-3�ã�x=1��$\sqrt{2}$���ɴ˼��������P���꣮
��� �⣺��1������������x�ύ�ڵ�A��-1��0����B��3��0�����㣬
�������ߵĺ�����ϵʽΪ��y=a��x+1����x-3����
����������y�ύ�ڵ�C��0��-3����
��-3=a��0+1����0-3����
��a=1��
�������ߵĺ�����ϵʽΪ��y=x2-2x-3��
�֡�y=��x-1��2-4��
�������ߵĶ�������Ϊ��1��-4����
��2������EM����EA��ED�ǡ�M���������ߣ�
��EA=ED��EA��AM��ED��MD��
���EAM�ա�EDM��HL����
�֡��ı���EAMD�����Ϊ4 $\sqrt{3}$��
��S��EAM=2 $\sqrt{3}$��
��$\frac{1}{2}$AM•AE=2 $\sqrt{3}$��
�֡�AM=2��
��AE=2 $\sqrt{3}$��
��ˣ���E������ΪE1��-1��2 $\sqrt{3}$����E2��-1��-2 $\sqrt{3}$����
��E���ڵڶ�����ʱ���е�D�ڵ�һ���ޣ�
��ֱ��������EAM�У�tan��EMA=$\frac{EA}{AM}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$��
���EMA=60�㣬
���DMB=60�㣬
���е�D��DF��AB������Ϊ��F��
��MF=1��DF=$\sqrt{3}$��
��ˣ��е�D������Ϊ��2��$\sqrt{3}$����
��ֱ��PD�ĺ�����ϵʽΪy=kx+b��
��E��-1��2 $\sqrt{3}$����D��2��$\sqrt{3}$������������ $\left\{\begin{array}{l}{-k+b=2\sqrt{3}}\\{2k+b=\sqrt{3}}\end{array}\right.$��
��֮���ã�$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=\frac{5\sqrt{3}}{3}}\end{array}\right.$��
���ԣ�ֱ��PD�ĺ�����ϵʽΪy=-$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$��
��E���ڵ�������ʱ���е�D�ڵ������ޣ�
ͬ�������е�D����Ϊ��2��-$\sqrt{3}$����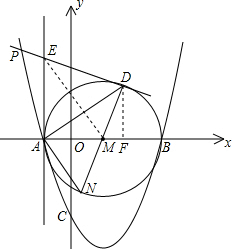
ֱ��PD�ĺ�����ϵʽΪy=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$��
��ˣ�ֱ��PD�ĺ�����ϵʽΪy=-$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$��y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$��
��3�����ı���EAMD��������ڡ�DAN�������
�֡�S�ı���EAMD=2S��EAM��S��DAN=2S��AMD��
��S��AMD=S��EAM��
��E��D���㵽x��ľ�����ȣ�
��PD���M����
���D���E��x��ͬ�࣬
������PD��x��ƽ�У�
��ʱ����PD�ĺ�����ϵʽΪy=2��y=-2��
��y=2ʱ����y=x2-2x-3�ã�x=1��$\sqrt{6}$��
��y=-2ʱ����y=x2-2x-3�ã�x=1��$\sqrt{2}$��
�����������ĵ�P��λ����4�����ֱ���P1��1+$\sqrt{6}$��2����P2��1-$\sqrt{6}$��2����P3��1+$\sqrt{2}$��-2����P4��1-$\sqrt{2}$��-2����
���� ���⿼����κ�����һ�κ�����Ӧ�á����ߵ����ʡ����߳�������ȫ�������ε��ж������ʡ�ͼ�����������Ҫ֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬���������ν�ϵ�˼�룬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
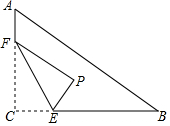 ��ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8����F�ڱ�AC�ϣ���AF=2����EΪ��BC�ϵĶ��㣬����CEF��ֱ��EF���ۣ���C���ڵ�P������P���߶�AB��ʱ���߶�PB�ij���Ϊ$\frac{44}{5}$-4$\sqrt{21}$��
��ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8����F�ڱ�AC�ϣ���AF=2����EΪ��BC�ϵĶ��㣬����CEF��ֱ��EF���ۣ���C���ڵ�P������P���߶�AB��ʱ���߶�PB�ij���Ϊ$\frac{44}{5}$-4$\sqrt{21}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
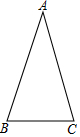 ��ͼ���ڡ�ABC�У�AB=AC����ABC=70�㣮
��ͼ���ڡ�ABC�У�AB=AC����ABC=70�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com