
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA=4��OC=3���Ҷ���A��C�����������ϣ�����M�ӵ�A��������ÿ��1����λ���ȵ��ٶ���AO���յ�O�ƶ�����N�ӵ�C������CB���յ�B��ͬ�����ٶ��ƶ��������������˶���x�루0��x��4��ʱ������N��NP��BC��BO�ڵ�P������MP��
��1��ֱ��д����B�����꣬�������P�����꣨�ú�x��ʽ�ӱ�ʾ����
��2������OMP�����ΪS����S��x֮��ĺ�������ʽ�����������ֵ�����S�����ֵ��
��3�������������˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ��OMP�ǵ��������Σ������ڣ����x��ֵ���������ڣ���˵�����ɣ�
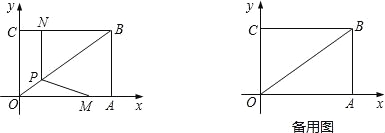
���𰸡���1��B��4��3����P��x��![]() x������2��S=��
x������2��S=��![]() x2+
x2+![]() x��0��x��4��, ���ֵΪ
x��0��x��4��, ���ֵΪ![]() ����3�����ڣ�x��ֵΪ
����3�����ڣ�x��ֵΪ![]() ���
���![]() ���
���![]() ��.
��.
��������
�����������1�����ݾ���OABC��OA=4��OC=3�Լ����ε����ʣ��ó�B�����꣬����PG��AB���ó���OPG�ס�OBA���������������ζ�Ӧ�߳ɱ����ó�P�����ꣻ��2������PG�Լ�OM�ij���ʾ����OMP��������ٸ��ݶ��κ���������������ֵ���ɣ���3����OMP�ǵ���������ʱ���������������PO=PM����OP=OM����OM=PM������ͼ�Σ��ֱ�������ɣ�
�����������1��������OABC�У�OA=4��OC=3����B������Ϊ��4��3������ͼ���ӳ�NP����OA�ڵ�G����PG��AB��OG=CN=x����PG��AB�����OPG�ס�OBA����![]() ����
����![]() =
=![]() ����ã�PG=
����ã�PG=![]() x������P������Ϊ��x��
x������P������Ϊ��x��![]() x������2��������OMP�У�OM=4��x��OM���ϵĸ�Ϊ
x������2��������OMP�У�OM=4��x��OM���ϵĸ�Ϊ![]() x����S=
x����S=![]() ��4��x��
��4��x��![]() x=��
x=��![]() x2+
x2+![]() x����S��x֮��ĺ�������ʽΪS=��
x����S��x֮��ĺ�������ʽΪS=��![]() x2+
x2+![]() x��0��x��4�����䷽����S=��
x��0��x��4�����䷽����S=��![]() ��x��2��2+
��x��2��2+![]() ������x=2ʱ��S�����ֵ�����ֵΪ
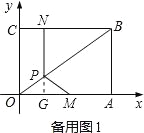
������x=2ʱ��S�����ֵ�����ֵΪ![]() ����3������ijһʱ�̣�ʹ��OMP�ǵ��������Σ��������£����籸��ͼ1������P��PG��AO�ڵ�G����PO=PM����OG=GM=CN=x����3x=4����ã�x=
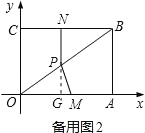
����3������ijһʱ�̣�ʹ��OMP�ǵ��������Σ��������£����籸��ͼ1������P��PG��AO�ڵ�G����PO=PM����OG=GM=CN=x����3x=4����ã�x=![]() �����籸��ͼ2������P��PG��AO�ڵ�G����OP=OM��CN=x����OP= OM= 4��x���ɹ��ɶ�������OB=
�����籸��ͼ2������P��PG��AO�ڵ�G����OP=OM��CN=x����OP= OM= 4��x���ɹ��ɶ�������OB=![]() =
=![]() =5����NP��OC����
=5����NP��OC����![]() ����
����![]() ����OP=
����OP=![]() x����
x����![]() x=4��x����ã�x=
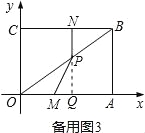
x=4��x����ã�x=![]() �����籸��ͼ3������P��PQ��OA������ΪQ����OM=PMʱ����PM=OM=4��x��OQ=CN=x����MQ=x-(4-x)=2x��4����Rt��MPQ�У�PQ2+QM2=MP2������
�����籸��ͼ3������P��PQ��OA������ΪQ����OM=PMʱ����PM=OM=4��x��OQ=CN=x����MQ=x-(4-x)=2x��4����Rt��MPQ�У�PQ2+QM2=MP2������![]() x��2+��2x��4��2=��4��x��2����ã�x=
x��2+��2x��4��2=��4��x��2����ã�x=![]() ��������������x��ֵΪ
��������������x��ֵΪ![]() ���
���![]() ���
���![]() ��ʱ����OMP�ǵ��������Σ�
��ʱ����OMP�ǵ��������Σ�



 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
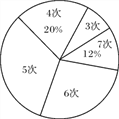
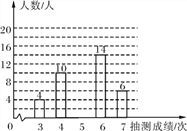
����Ŀ��Ϊ���˽�ijУ���꼶���������������������ʦ�����ȡ�������������������ϲ��ԣ����Գɼ�������ͳ�ƣ����Ƴ����µ�����ͳ��ͼ��
��1���γ���������������������ͳ��ͼ����������
��2�����ⲿ������������ݵ���������λ����
(3)���涨��������5������(��5��)Ϊ���ܴ�꣬���У350�����꼶�����й����ж��������ܴ�꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������m��nΪ������ʮλ������m����λ������n����λ������ ____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������38����ѧ���������꼶ѧ����6 858����Ϊ���˽�õ������꼶ѧ��ÿ������������ʱ�䣬����������ѧ��ͳ��֪ʶ�����������������Ҫ�����ļ�����Ҫ����������ٳ������飻����Ƶ����ʾ������������������壻���������ݣ��ݷ������ݣ�������ȷ���ǣ�������
A. �٢ڢۢܢ� B. �ڢ٢ۢܢ� C. �ڢ٢ܢۢ� D. �ڢ٢ܢݢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���B=90�㣬AB=6������ABCƽ������DEF��λ�ã����ı���DGCF�����Ϊ15����DG=4����CF= �� 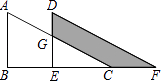
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ѧ��ͳ��ijһ��˯����ѧϰ������Է����������õ�ʱ����һ������ռ�İٷֱȣ�ѡ��_____ͳ��ͼ��Ϊ���ʣ������ͳ��һ��ҹ�����±仯�����ѡ��_____ͳ��ͼ��Ϊ���ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ�зֱ���к������������������������������������ĸ�С�����ֲ�֮ͬ�⣬С��û���κ�����ÿ������ǰ�Ƚ������������
��1����������ȡһ�������ϵĺ��ָպ����������ĸ���Ϊ���٣�
��2��Сӱ������ȡһ���º��ֺ�Żش��У�Ȼ���ٴ�����ȡһ����Сӱȡ�����������Ϻ���ǡ��������Ҹ��������ij����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
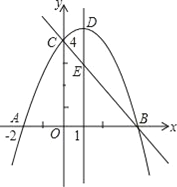
����Ŀ����ͼ��������y=ax2+bx+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A�͵�B�����е�A������Ϊ����2��0���������ߵĶԳ���x=1�������߽��ڵ�D����ֱ��BC���ڵ�E��
��1���������ߵĽ���ʽ��
��2������F��ֱ��BC�Ϸ����������ϵ�һ�����㣬�Ƿ���ڵ�Fʹ�ı���ABFC�����Ϊ17�������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
��3��ƽ����DE��һ����ֱ��l��ֱ��BC�ཻ�ڵ�P�����������ཻ�ڵ�Q������D��E��P��QΪ������ı�����ƽ���ı��Σ����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com