练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知4×16m×64m=421 ， 求（﹣m2）3÷（m3m2）的值．

    【答案】解：∵4×16m×64m=421 ， ∴41+2m+3m=421 ，
    ∴5m+1=21，
    ∴m=4，
    ∴（﹣m2）3÷（m3m2）
    =﹣m6÷m5
    =﹣m
    =﹣4．
    【解析】先根据幂的乘方和积的乘方得出5m+1=21，求出m的值，再算乘方，算除法，最后代入求出即可．
    【考点精析】关于本题考查的同底数幂的乘法和同底数幂的除法，需要了解同底数幂的乘法法则aman=am+n(m,n都是正数)；同底数幂的除法法则：am÷an=am-n（a≠0，m，n都是正整数，且m＞n）才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】今夏，十堰市王家河村瓜果喜获丰收，果农王二胖收获西瓜20吨，香瓜12吨，现计划租用甲、乙两种货车共8辆将这批瓜果全部运往外地销售，已知一辆甲种货车可装西瓜4吨和香瓜1吨，一辆乙种货车可装西瓜和香瓜各2吨．
    （1）果农王二胖如何安排甲、乙两种货车可一次性地运到销售地？有几种方案？
    （2）若甲种货车每辆要付运输费300元，乙种货车每辆要付运输费240元，则果农王二胖应选择哪种方案，使运输费最少？最少运费是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有一张圆心角为108°，半径为4cm的扇形纸片，小红剪去圆心角为θ的部分扇形纸片后，将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽（接缝处不重叠），则剪去的扇形纸片的面积为（ ）.

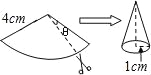
    A．0.8πcm2 B．3.2πcm2 C．4πcm2 D．4.8πcm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠AOB=40°，在∠AOB的两边OA、OB上分别存在点Q、点P，过点Q作直线QR∥OB，当OP=QP时，∠PQR的度数是（ ）.

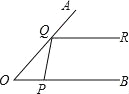
    A．60° B．80° C．100° D．120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形OABC的边OA=4，OC=3，且顶点A、C均在坐标轴上，动点M从点A出发，以每秒1个单位长度的速度沿AO向终点O移动；点N从点C出发沿CB向终点B以同样的速度移动，当两个动点运动了x秒（0＜x＜4）时，过点N作NP⊥BC交BO于点P，连接MP．

    （1）直接写出点B的坐标，并求出点P的坐标（用含x的式子表示）；

    （2）设△OMP的面积为S，求S与x之间的函数表达式；若存在最大值，求出S的最大值；

    （3）在两个动点运动的过程中，是否存在某一时刻，使△OMP是等腰三角形？若存在，求出x的值；若不存在，请说明理由．

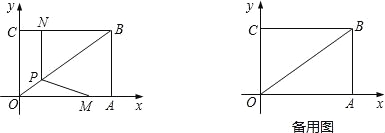
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边△ABC中，点D，E分别在边BC，AB上，且BD=AE，AD与CE交于点F．

    （1）求证：AD=CE；

    （2）求∠DFC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程kx2+2x+1＝0有实数根，则实数k的取值范围是（　　）

    A.k≤1B.k＜1C.k≤1且k≠0D.k＜1且k≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

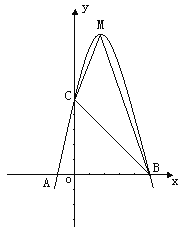
    【题目】已知：二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.

    （1)求抛物线的解析式；

    (2)求△MCB的面积S△MCB.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】由四舍五入得到的近似数－8.30×104，精确到(　　)

    A. 百分位 B. 十分位

    C. 千位 D. 百位

    查看答案和解析>>

    同步练习册答案