
【题目】已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.求证:(1)BD=AE.(2)若线段AD=5,AB=17,求线段ED的长。

【答案】(1)、证明过程见解析;(2)、13.
【解析】试题分析:(1)、根据等腰直角三角形的性质得出AC=BC,CD=CE,∠ACD=∠DCE=90°,从而说明∠ACE=∠BCD,然后根据SAS判定三角形全等,从而得到BD=AE;(2)、根据题意得出BD的长度,根据全等从而得到AE的长度以及∠EAD为直角,然后利用Rt△AED的勾股定理求出DE的长度.
试题解析:(1)、∵△ABC和△ECD都是等腰直角三角形, ∴AC=BC,CD=CE, ∵∠ACD=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD, ∴∠ACE=∠BCD,
在△ACE和△BCD中,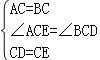 , ∴△ACE≌△BCD(SAS), ∴BD=AE.
, ∴△ACE≌△BCD(SAS), ∴BD=AE.
(2)、∵AD="5," AB="17," ∴BD=17-5=12 ∵△ABC是等腰直角三角形
∴∠B=45°由(1)可知△ACE≌△BCD ∴∠EAC=∠B=45° AE=BD=7
∴∠EAD=90° ∴ED=![]()


科目:初中数学 来源: 题型:
【题目】深圳今年4月份某星期的最高气温如下(单位℃):26,25,27,28,27,25,25,则这个星期的最高气温的众数和中位数分别是( )
A.25,26 B.25,26.5 C.27,26 D.25,28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣4).
的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣4).
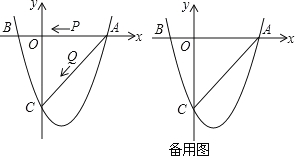
(1)求该二次函数的解析;
(2)若点P、Q同时从A点出发,以每秒1个单位长度的速度分别沿AB、AC边运动,其中一点到达端点时,另一点也随之停止运动.
①当点P运动到B点时,在x轴上是否存在点E,使得以A、E、Q为顶点的三角形为等腰三角形?若存在,请求出E点的坐标;若不存在,请说明理由.
②当P、Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请直接写出t的值及D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
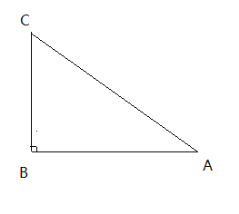
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm。
(1)若P、Q是△ABC边上的两个动点,其中点P从A沿A→B方向运动,速度为每秒1cm,点Q从B沿B→C方向运动,速度为每秒2cm,两点同时出发,设出发时间为t秒.(1)、当t=1秒时,求PQ的长;(2)、从出发几秒钟后,△PQB是等腰三角形?(3)、若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动,则当点M在边CA上运动时,求△BCM成为等腰三角形时M运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】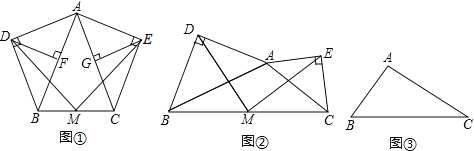
如图①,在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图①所示,其中,DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD,ME,MF,MG.则下列结论正确的是__________(填写序号)
①四边形AFMG是菱形;②△DFM和△EGM都是等腰三角形;③MD=ME;④MD⊥ME.
(2)数学思考:
如图②,在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量和位置关系?请给出证明过程.
(3)类比探究:如图③Rt△ABC中,斜边BC=10,AB=6,分别以AB、AC为斜边作等腰直角三角形ABD和ACE,请直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
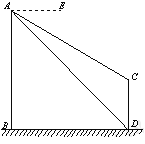
(1)求两建筑物两底部之间的水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com