
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
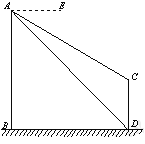
(1)求两建筑物两底部之间的水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
【答案】(1)60米;(2)![]() 米.
米.
【解析】
试题分析:(1)根据平行线的性质可以得到:∠BAD=∠ADB=45°,根据等腰直角三角形的性质可以求出BD的长度;
(2)延长AE、DC交于点F,可知四边形ABDF是正方形,根据tan∠CAF=![]() ,求出CF的长度,再根据DF的长度求出CD的高度.
,求出CF的长度,再根据DF的长度求出CD的高度.
试题解析:(1)根据题意得BD∥AE,
∴∠ADB=∠EAD=45°.
∵∠ABD=90°,
∴∠BAD=∠ADB=45°.
∴BD=AD=60(米).
∴两建筑物两底部之间的水平距离BD的长度为60米
(2)延长AE、DC交于点F,
根据题意可知四边形ABDF是正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
由tan∠CAF=![]() ,
,
得CF=AFtan∠CAF
=60tan30°
=60×![]() =20
=20![]() .
.
又∵DF=60,
∴CD=60-20![]() .
.
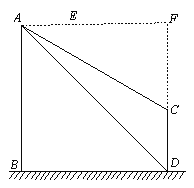
∴建筑物CD的高度为(60-20![]() )米.
)米.


科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.求证:(1)BD=AE.(2)若线段AD=5,AB=17,求线段ED的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
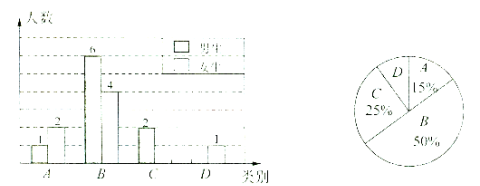
(l) 王老师一共调查了多少名同学?
(2) C类女生有多少名?D类男生有多少名?并将上面条形统计图补充完整;
(3) 为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学中男同学不少于1人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有16名工人,每人每天可加工甲种零件5个或乙种零件4个.在这16名工人中,一部分人加工甲种零件,其余的加工乙种零件.已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元.若此车间一共获利1 440元,求这一天有几名工人加工甲种零件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.
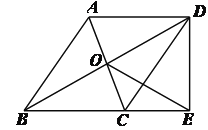
(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD ![]() CE=CD
CE=CD ![]() DE.
DE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com