
ЁОЬтФПЁП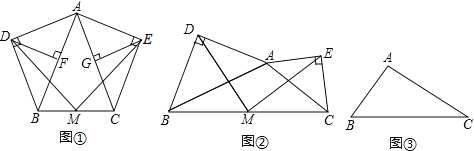
ШчЭМЂйЃЌдкЕШбќЁїABCжаЃЌAB=ACЃЌЗжБ№вдABКЭACЮЊаББпЃЌЯђЁїABCЕФЭтВрзїЕШбќжБНЧШ§НЧаЮЃЌШчЭМЂйЫљЪОЃЌЦфжаЃЌDFЁЭABгкЕуFЃЌEGЁЭACгкЕуGЃЌMЪЧBCЕФжаЕуЃЌСЌНгMDЃЌMEЃЌMFЃЌMGЃЎдђЯТСаНсТле§ШЗЕФЪЧ__________ЃЈЬюаДађКХЃЉ
ЂйЫФБпаЮAFMGЪЧСтаЮЃЛЂкЁїDFMКЭЁїEGMЖМЪЧЕШбќШ§НЧаЮЃЛЂлMD=MEЃЛЂмMDЁЭMEЃЎ
ЃЈ2ЃЉЪ§бЇЫМПМЃК
ШчЭМЂкЃЌдкШЮвтЁїABCжаЃЌЗжБ№вдABКЭACЮЊаББпЃЌЯђЁїABCЕФЭтВрзїЕШбќжБНЧШ§НЧаЮЃЌMЪЧBCЕФжаЕуЃЌСЌНгMDКЭMEЃЌдђMDгыMEОпгадѕбљЕФЪ§СПКЭЮЛжУЙиЯЕЃПЧыИјГіжЄУїЙ§ГЬЃЎ
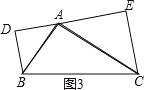
ЃЈ3ЃЉРрБШЬНОПЃКШчЭМЂлRtЁїABCжаЃЌаББпBC=10ЃЌAB=6ЃЌЗжБ№вдABЁЂACЮЊаББпзїЕШбќжБНЧШ§НЧаЮABDКЭACEЃЌЧыжБНгаДГіDEЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЂкЂлЂмЃЛЃЈ2ЃЉ![]() жЄУїМћНтЮіЃЛЃЈ3ЃЉDEЕФГЄЮЊЃК
жЄУїМћНтЮіЃЛЃЈ3ЃЉDEЕФГЄЮЊЃК![]() Лђ
Лђ![]() ,
,![]() .
.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЬѕМўПЩвдЭЈЙ§Ш§НЧаЮШЋЕШКЭжсЖдГЦЕФаджЪЃЌжБНЧШ§НЧаЮаББпЩЯЕФжаЯпаджЪвдМАЫФЕуЙВдВМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉШЁABЁЂACЕФжаЕуFЁЂGЃЌСЌНгDFЃЌMFЃЌEGЃЌMGЃЌИљОнШ§НЧаЮЕФжаЮЛЯпЕФаджЪКЭЕШбќжБНЧШ§НЧаЮЕФаджЪОЭПЩвдЕУГіЫФБпаЮAFMGЪЧЦНааЫФБпаЮЃЌДгЖјЕУГіЁїDFMЁеЁїMGEЃЌИљОнЦфаджЪвдМАИїИіНЧжЎМфЕФЙиЯЕМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЗжЫФжжЧщПіЃЌЂйЕШбќжБНЧШ§НЧаЮABDКЭACEЖМдкRtЁїABCЭтВрЃЌЂкЕШбќжБНЧШ§НЧаЮABDКЭACEЖМдкRtЁїABCФкВрЃЌЂлЕШбќжБНЧШ§НЧаЮABDКЭACEвЛИіRtЁїABCЭтВрЃЌЂмЕШбќжБНЧШ§НЧаЮABDКЭACE,вЛИідкRtЁїABCЭтВрЃЌвЛИідкЕШбќжБНЧШ§НЧаЮABDКЭACEЖМдкRtЁїABCФкВрЗжБ№ЧѓГіDEЕФГЄЖШМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁп![]() КЭ
КЭ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]()
![]() Ёпдк
Ёпдк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ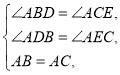
![]()
![]()
![]() гкЕуFЃЌ
гкЕуFЃЌ![]() гкЕуGЃЌ
гкЕуGЃЌ![]()
![]()
![]()
![]() Ёр
Ёр![]() КЭ
КЭ![]() ЖМЪЧЕШбќШ§НЧаЮЃЌЙЪЂке§ШЗЃЛ ЁпMЪЧBCЕФжаЕуЃЌЁр
ЖМЪЧЕШбќШ§НЧаЮЃЌЙЪЂке§ШЗЃЛ ЁпMЪЧBCЕФжаЕуЃЌЁр ![]()
![]() Ёр
Ёр![]()
![]() МД
МД![]() дк
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ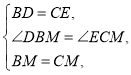
![]()
![]() ЙЪЂле§ШЗЃЛСЌНгAMЁЂFMЁЂGMЃЌШчЭМ1ЫљЪОЃК
ЙЪЂле§ШЗЃЛСЌНгAMЁЂFMЁЂGMЃЌШчЭМ1ЫљЪОЃК
![]() MЪЧBCЕФжаЕуЃЌ
MЪЧBCЕФжаЕуЃЌ![]()
![]()
![]()
![]()
![]()
![]() ЁрЫФБпаЮAFMGЪЧСтаЮЃЌЙЪЂйе§ШЗЃЛ
ЁрЫФБпаЮAFMGЪЧСтаЮЃЌЙЪЂйе§ШЗЃЛ![]() MЪЧBCЕФжаЕуЃЌ
MЪЧBCЕФжаЕуЃЌ![]()
![]()
![]() ЁрЫФБпаЮADBMЫФЕуЙВдВЃЌ
ЁрЫФБпаЮADBMЫФЕуЙВдВЃЌ![]() ЁпAMЪЧЖдГЦжс,
ЁпAMЪЧЖдГЦжс,![]()
![]()
![]() ЙЪЂме§ШЗЃЌЙЪД№АИЮЊЃКЂйЂкЂлЂмЃЛ
ЙЪЂме§ШЗЃЌЙЪД№АИЮЊЃКЂйЂкЂлЂмЃЛ
ЃЈ2ЃЉ![]() РэгЩШчЯТЃКШЁABЁЂACЕФжаЕуFЁЂGЃЌСЌНгDFЃЌMFЃЌEGЃЌMGЃЌШчЭМ2ЫљЪОЃК
РэгЩШчЯТЃКШЁABЁЂACЕФжаЕуFЁЂGЃЌСЌНгDFЃЌMFЃЌEGЃЌMGЃЌШчЭМ2ЫљЪОЃК
![]() ЁпЁїABDКЭЁїAECЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпЁїABDКЭЁїAECЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]()
![]()
![]()
![]() ЁпMЪЧBCЕФжаЕуЃЌ
ЁпMЪЧBCЕФжаЕуЃЌ![]() ЁрЫФБпаЮAFMGЪЧЦНааЫФБпаЮЃЌ
ЁрЫФБпаЮAFMGЪЧЦНааЫФБпаЮЃЌ![]()
![]()
![]()
![]()
![]() Ёпдк
Ёпдк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)![]() жаЃЌаББпBC=10ЃЌAB=6ЃЌЁрAC=8ЃЌ
жаЃЌаББпBC=10ЃЌAB=6ЃЌЁрAC=8ЃЌ![]() КЭ
КЭ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]()
![]() ЗжЫФжжЧщПіЃЌЂйШчЭМ3ЃЌ
ЗжЫФжжЧщПіЃЌЂйШчЭМ3ЃЌ![]() КЭ
КЭ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]()
![]()
![]() ЁрDЃЌAЃЌEШ§ЕуЙВЯпЃЌ
ЁрDЃЌAЃЌEШ§ЕуЙВЯпЃЌ![]() ЂкШчЭМ4ЃЌ
ЂкШчЭМ4ЃЌ![]() КЭ
КЭ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]()
![]() ЁрЕуAЃЌDЃЌEЙВЯпЃЌ
ЁрЕуAЃЌDЃЌEЙВЯпЃЌ![]() ЂлШчЭМ5ЃЌ
ЂлШчЭМ5ЃЌ![]() КЭ
КЭ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]()
![]()
![]()
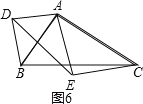
![]() ЂмШчЭМ6ЃЌ
ЂмШчЭМ6ЃЌ![]() КЭ
КЭ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]()
![]()
![]()
![]() злЩЯЫљЪіЃКDEЕФГЄЮЊЃК
злЩЯЫљЪіЃКDEЕФГЄЮЊЃК![]() Лђ
Лђ![]() ,
,![]() .
.





 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋХзЮяЯпy=x2ЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ3ИіЕЅЮЛЃЌдђЕУЕНЕФХзЮяЯпНтЮіЪНЪЧЃЈЁЁЁЁЃЉ
A.y=ЃЈxЉ2ЃЉ2Љ3
B.y=ЃЈxЉ2ЃЉ2+3
C.y=ЃЈx+2ЃЉ2Љ3
D.y=ЃЈx+2ЃЉ2+3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСавђЪНЗжНтДэЮѓЕФЪЧ( )
A. 2axЃaЃНa(2xЃ1)B. x2Ѓ2xЃЋ1ЃН(xЃ1)2
C. 4ax2ЃaЃНa(2xЃ1)2D. ax2ЃЋ2axЃ3aЃНa(xЃ1)(xЃЋ3)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌЁїABCКЭЁїECDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯACD=ЁЯDCE=90ЁуЃЌDЮЊABБпЩЯвЛЕуЃЎЧѓжЄЃК(1)BD=AEЃЎ(2)ШєЯпЖЮAD=5,AB=17,ЧѓЯпЖЮEDЕФГЄЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЏМђЃК(1) x2yЃ3xy2ЃЋ2yx2Ѓy2xЃЛ(2)ЃЈЃabЃЋ2a)Ѓ(3aЃab).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК(1) Ѓ3ЃЋ5.3ЃЋ7Ѓ5.3 (2) 0.35ЃЋ(Ѓ0.6)ЃЋ0.25ЃЋ(Ѓ5.4)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОХФъМЖЃЈ1ЃЉАр40УћЭЌбЇжаЃЌ14ЫъЕФга1ШЫЃЌ15ЫъЕФга21ШЫЃЌ16ЫъЕФга16ШЫЃЌ17ЫъЕФга2ШЫЃЌдђетИіАрЭЌбЇФъСфЕФжаЮЛЪ§ЪЧ ЫъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуЃЈ1ЃЌ2ЃЉЮЛгкЕкЁЁ ЁЁЯѓЯоЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com