
【题目】某大型超市的采购人员先后购进两批晋祠大米,购进第一批大米共花费5400元,进货单价为m元/千克,该超市将其中3000千克优等品以进货单价的两倍对外出售,余下的二等品则以1.5元/千克的价格出售.当第一批大米全部售出后,花费5000元购进了第二批大米,这一次的进货单价比第一批少了0.2元.其中优等品占总重量的一半,超市以2元/千克的单价出售优等品,余下的二等品在这批进货单价的基础上每千克加价0.6元后全部卖完,若不计其他成本,则售完第二批大米获得的总利润是4000元(总售价﹣总进价=总利润)
(1)用含m的代数式表示第一批大米的总利润.
(2)求第一批大米中优等品的售价.
【答案】(1)6000m+![]() ﹣9900;(2)2.4元.
﹣9900;(2)2.4元.
【解析】
试题分析:(1)用总销售额减去成本即可求出毛利润;(2)设第一批进货单价为m元/千克,则第二批的进货单价为(m﹣2)元/千克,根据第二批大米获得的毛利润是4000元,列方程求解.
试题解析:(1)由题意得,总利润为:3000×2m+1.5×(![]() ﹣3000)﹣5400=6000m+
﹣3000)﹣5400=6000m+![]() ﹣9900;(2)设第一批进货单价为m元/千克,由题意得,
﹣9900;(2)设第一批进货单价为m元/千克,由题意得,![]() ×
×![]() ×2+
×2+![]() ×
×![]() ×(m﹣0.2+0.6)﹣5000=4000,解得:m=1.2,经检验:m=1.2是原分式方程的解,且符合题意.则优等品的售价为:2m=2.4.所以第一批大米中优等品的售价是2.4元.
×(m﹣0.2+0.6)﹣5000=4000,解得:m=1.2,经检验:m=1.2是原分式方程的解,且符合题意.则优等品的售价为:2m=2.4.所以第一批大米中优等品的售价是2.4元.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】甲班有45人,乙班有39人.现在需要从甲、乙班各抽调一些同学去参加歌咏比赛.如果从甲班抽调的人数比乙班多1人,那么甲班剩余人数恰好是乙班剩余人数的2倍.请问从甲、乙两班各抽调了多少人参加歌咏比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.
结论1:DM、MN的数量关系是 ;
结论2:DM、MN的位置关系是 ;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查八年级部分女生;
方案二:调查八年级部分男生;
方案三:到八年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整; 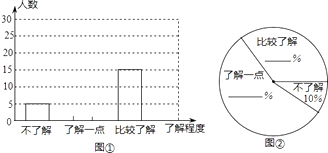
(3)请你估计该校八年级约有多少名学生比较了解“低碳”知识.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为 :P,即P=|x|+|y|(其中“+”是四则运算中的加法).
(1)求点A(-1,3),B(![]() +2,
+2, ![]() -2)的勾股值A、B;
-2)的勾股值A、B;
(2)求满足条件N=3的所有点N围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(﹣1)2012+(π﹣3.14)0﹣(﹣ ![]() )﹣1
)﹣1
(2)化简求值:(2x+y)2﹣(2x﹣y)(x+y)﹣2(x﹣2y)(x+2y),其中x= ![]() ,y=﹣2.
,y=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数解析式:h=﹣3(t﹣2)2+5,则小球距离地面的最大高度是( )
A.2米
B.3米
C.5米
D.6米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com