
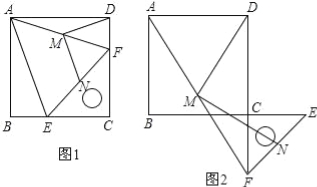
【题目】操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.
结论1:DM、MN的数量关系是 ;
结论2:DM、MN的位置关系是 ;
拓展与探究:
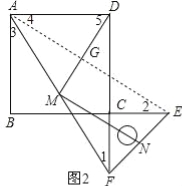
(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.

【答案】(1)证明参见解析;(2)相等,垂直;(3)成立,理由参见解析.
【解析】
试题分析:(1)根据正方形的性质以及等腰直角三角形的知识证明出CE=CF,继而证明出△ABE≌△ADF,得到AE=AF,从而证明出△AEF是等腰三角形;(2)DM、MN的数量关系是相等,利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直,利用三角形外角性质和等腰三角形两个底角相等性质,及全等三角形对应角相等即可得出结论;(3)成立,连接AE,交MD于点G,标记出各个角,首先证明出MN∥AE,MN=![]() AE,利用三角形全等证出AE=AF,而DM=
AE,利用三角形全等证出AE=AF,而DM=![]() AF,从而得到DM,MN数量相等的结论,再利用三角形外角性质和三角形全等,等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°.从而得到DM、MN的位置关系是垂直.
AF,从而得到DM,MN数量相等的结论,再利用三角形外角性质和三角形全等,等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°.从而得到DM、MN的位置关系是垂直.
试题解析:(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠ADF=90°,∵△CEF是等腰直角三角形,∠C=90°,∴CE=CF,∴BC﹣CE=CD﹣CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,∴△AEF是等腰三角形;(2)DM、MN的数量关系是相等,DM、MN的位置关系是垂直;∵在Rt△ADF中DM是斜边AF的中线,∴AF=2DM,∵MN是△AEF的中位线,∴AE=2MN,∵AE=AF,∴DM=MN;∵∠DMF=∠DAF+∠ADM,AM=MD,∵∠FMN=∠FAE,∠DAF=∠BAE,∴∠ADM=∠DAF=∠BAE,∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°,∴DM⊥MN;(3)(2)中的两个结论还成立,连接AE,交MD于点G,∵点M为AF的中点,点N为EF的中点,∴MN∥AE,MN=![]() AE,由已知得,AB=AD=BC=CD,∠B=∠ADF,CE=CF,又∵BC+CE=CD+CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,在Rt△ADF中,∵点M为AF的中点,∴DM=
AE,由已知得,AB=AD=BC=CD,∠B=∠ADF,CE=CF,又∵BC+CE=CD+CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,在Rt△ADF中,∵点M为AF的中点,∴DM=![]() AF,∴DM=MN,∵△ABE≌△ADF,∴∠1=∠2,∵AB∥DF,∴∠1=∠3,同理可证:∠2=∠4,∴∠3=∠4,∵DM=AM,∴∠MAD=∠5,∴∠DGE=∠5+∠4=∠MAD+∠3=90°,∵MN∥AE,∴∠DMN=∠DGE=90°,∴DM⊥MN.所以(2)中的两个结论还成立.
AF,∴DM=MN,∵△ABE≌△ADF,∴∠1=∠2,∵AB∥DF,∴∠1=∠3,同理可证:∠2=∠4,∴∠3=∠4,∵DM=AM,∴∠MAD=∠5,∴∠DGE=∠5+∠4=∠MAD+∠3=90°,∵MN∥AE,∴∠DMN=∠DGE=90°,∴DM⊥MN.所以(2)中的两个结论还成立.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】统计2010年上海世博会前20天日参观人数,得到如下频数分布表和频数分布直方图(部分未完成): 上海世博会前20天日参观人数的频数分布表:
组别(万人) | 组中值(万人) | 频数 |
7.5~14.5 | 11 | 5 |
14.5~21.5 | 6 | |
21.5~28.5 | 25 | |
28.5~35.5 | 32 | 3 |
上海世博会前20天日参观人数的频数分布直方图: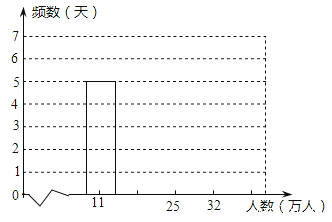
(1)请补全频数分布表和频数分布直方图;
(2)求出日参观人数不低于22万的天数和所占的百分比;
查看答案和解析>>
科目:初中数学 来源: 题型:
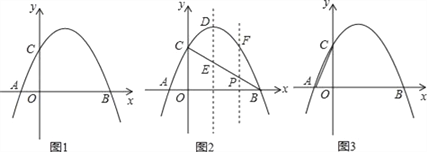
【题目】如图1,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)如图2,连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;用含m的代数式表示线段PF的长;并求出当m为何值时,四边形PEDF为平行四边形?
(3)如图3,连接AC,在x轴上是否存在点Q,使△ACQ为等腰三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市的采购人员先后购进两批晋祠大米,购进第一批大米共花费5400元,进货单价为m元/千克,该超市将其中3000千克优等品以进货单价的两倍对外出售,余下的二等品则以1.5元/千克的价格出售.当第一批大米全部售出后,花费5000元购进了第二批大米,这一次的进货单价比第一批少了0.2元.其中优等品占总重量的一半,超市以2元/千克的单价出售优等品,余下的二等品在这批进货单价的基础上每千克加价0.6元后全部卖完,若不计其他成本,则售完第二批大米获得的总利润是4000元(总售价﹣总进价=总利润)
(1)用含m的代数式表示第一批大米的总利润.
(2)求第一批大米中优等品的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=![]() x+m与x轴交于A点,且经过点B(﹣
x+m与x轴交于A点,且经过点B(﹣![]() ,2).已知抛物线C:y=ax2+bx+9与x轴只有一个公共点,恰为A点.
,2).已知抛物线C:y=ax2+bx+9与x轴只有一个公共点,恰为A点.
(1)求m的值及∠BAO的度数;
(2)求抛物线C的函数表达式;
(3)将抛物线C沿x轴左右平移,记平移后的抛物线为C1,其顶点为P.
平移后,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C1上?
如能,求出此时顶点P的坐标;如不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com