
����Ŀ����ͼ��ֱ��l��y=![]() x+m��x�ύ��A�㣬�Ҿ�����B����
x+m��x�ύ��A�㣬�Ҿ�����B����![]() ��2������֪������C��y=ax2+bx+9��x��ֻ��һ�������㣬ǡΪA�㣮
��2������֪������C��y=ax2+bx+9��x��ֻ��һ�������㣬ǡΪA�㣮
��1����m��ֵ����BAO�Ķ�����
��2����������C�ĺ�������ʽ��
��3����������C��x������ƽ�ƣ���ƽ�ƺ��������ΪC1���䶥��ΪP��
ƽ�ƺ���PAB��ֱ��AB���۵õ���DAB����D�ܷ�����������C1�ϣ�
���ܣ������ʱ����P�����ꣻ�粻�ܣ�˵�����ɣ�

���𰸡���1��m=3����BAO=30������2��y=![]() ��x+3
��x+3![]() ��2����3���ܣ�P������Ϊ��21
��2����3���ܣ�P������Ϊ��21![]() ��0����
��0����
��������
�����������1����B���������ֱ��l�Ľ���ʽ�������m��ֵ�����ֱ��l�Ľ���ʽ����ֱ��l��y�ύ�ڵ�C�����C�����������������Ǻ������������BAO�Ķ�������2��������֪�������߱ض�����0��9������������x��ֻ��һ��������A����A���������ߵĶ��㣬���Կ����������ߵĶ���ʽy=a��x+3![]() ��2������0��9�����붥��ʽ�������a��ֵ����3����P������Ϊ��h��0����������֪����P������A����࣬���Ե�P��A���Ҳ࣬���ڵ�P��D����AB�Գƣ��ҵ�D��������������C1�ϣ��������D���������������C1�Ľ���ʽ�������h��ֵ��
��2������0��9�����붥��ʽ�������a��ֵ����3����P������Ϊ��h��0����������֪����P������A����࣬���Ե�P��A���Ҳ࣬���ڵ�P��D����AB�Գƣ��ҵ�D��������������C1�ϣ��������D���������������C1�Ľ���ʽ�������h��ֵ��
�����������1����B����![]() ��2������y=
��2������y=![]() x+m����2=��1+m����m=3����ֱ��l�Ľ���ʽΪy=
x+m����2=��1+m����m=3����ֱ��l�Ľ���ʽΪy=![]() x+3����ֱ��l��y�ύ�ڵ�C,��x=0����y=
x+3����ֱ��l��y�ύ�ڵ�C,��x=0����y=![]() x+3����y=3����C������Ϊ��0��3������y=0����y=
x+3����y=3����C��������0��3������y=0����y=![]() x+3����x=��3
x+3����x=��3![]() ����A����������3
����A����������3![]() ��0������OC=3��OA=3
��0������OC=3��OA=3![]() ����tan��BAO=
����tan��BAO=![]() =
=![]() �����BAO=30������2����x=0����y=ax2+bx+9����y=9,��������C������0��9��������������C��x��ֻ��һ�������㣬ǡΪA�㣬��A����������C�Ķ��㣬�������ߵĶ���ʽΪy=a��x+3
�����BAO=30������2����x=0����y=ax2+bx+9����y=9,��������C������0��9��������������C��x��ֻ��һ�������㣬ǡΪA�㣬��A����������C�Ķ��㣬�������ߵĶ���ʽΪy=a��x+3![]() ��2���ѣ�0��9������y=a��x+3
��2���ѣ�0��9������y=a��x+3![]() ��2����a=
��2����a=![]() ����������C�Ľ���ʽΪy=
����������C�Ľ���ʽΪy=![]() ��x+3
��x+3![]() ��2����3����������C1�Ľ���ʽΪy=
��2����3����������C1�Ľ���ʽΪy=![]() ��x��h��2������P��A�����ʱ����Dһ������������C1�ϣ���������������⣬����P��A���Ҳ�ʱ����ʱ��P��h��0����AP=h+3
��x��h��2������P��A�����ʱ����Dһ������������C1�ϣ���������������⣬����P��A���Ҳ�ʱ����ʱ��P��h��0����AP=h+3![]() ���ɶԳ��Կ�֪��AD=AP=h+3
���ɶԳ��Կ�֪��AD=AP=h+3![]() ����DAB=��PAB=30��������D��DE��x���ڵ�E����AE=
����DAB=��PAB=30��������D��DE��x���ڵ�E����AE=![]() AD=
AD=![]() ��DE=
��DE=![]() AE=
AE=![]() ����D��������
����D��������![]() ��
��![]() ������D��
������D��![]() ��
��![]() ������y=
������y=![]() ��x��h��2����
��x��h��2����![]() =
=![]() ��
��![]() ��2����h=21
��2����h=21![]() ��h=��3
��h=��3![]() ����h=��3
����h=��3![]() ʱ����ʱP��A�غϣ�������������⣬����������P������Ϊ��21
ʱ����ʱP��A�غϣ�������������⣬����������P������Ϊ��21![]() ��0����
��0����





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֤������ͼ1����һ����45���ǵ�ֱ�����ǰ�ECF��һ��������ABCD�ڷ���һ��ʹ���ǰ��ֱ�Ƕ���������εĶ���C�غϣ���E��F�ֱ��������εı�CB��CD�ϣ�����AF��ȡAF�е�M��EF���е�N������MD��MN��
��1������AE����֤����AEF�ǵ��������Σ�
�����뷢�֣�
��2���ڣ�1���������£����ж�MD��MN��������ϵ��λ�ù�ϵ���ó����ۣ�
����1��DM��MN��������ϵ�� ��
����2��DM��MN��λ�ù�ϵ�� ��
��չ��̽����
��3����ͼ2����ͼ1�е�ֱ�����ǰ�ECF�Ƶ�C˳ʱ����ת180���������������䣬��2���е��������ۻ��������������������֤����������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1������1��2012+����3.14��0������ ![]() ����1
����1
��2��������ֵ����2x+y��2����2x��y����x+y����2��x��2y����x+2y��������x= ![]() ��y=��2��
��y=��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һС���׳��������ĸ߶�h���ף��ͷ���ʱ��t���룩�������к�������ʽ��h=��3��t��2��2+5����С������������߶��ǣ� ��
A.2��
B.3��
C.5��
D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬʱ�ӹ�ij�������������������һ��ͣ�������豸�������豸�������Ĺ���Ч����ԭ����2�����������Լӹ����������![]() (��)��ʱ��
(��)��ʱ��![]() (ʱ)�ĺ���ͼ����ͼ��ʾ��
(ʱ)�ĺ���ͼ����ͼ��ʾ��

��1��������ӹ����������y��ʱ��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2���������ӹ��������![]() ��ֵ��
��ֵ��
��3���ס��������ӹ������������һ��װ�䣬ÿ��300��װһ�䣬���װ���ʱ����Բ��ƣ����ʱ��ǡ��װ����1�䣿�پ����ʱ��ǡ��װ����2�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��Բ���ĸ���4���ף���Բ������뾶r��cm���仯ʱ��Բ�������V��cm3��Ҳ��֮�仯�� 
��1��������仯�����У��Ա����� �� ������� ��
��2��Բ�������V�����뾶r�Ĺ�ϵʽ�� ��
��3����Բ���ĵ���뾶��2�仯��8ʱ��Բ���������cm3�仯��cm3 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
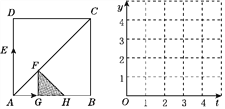
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4������E�ӵ�A��������ÿ��2����λ���ٶ���A��D��A�˶�������G�ӵ�A��������ÿ��1����λ���ٶ���A��B�˶�������һ���㵽���յ�ʱ����һ����֮Ҳֹͣ�˶�������G��FG��AB��AC�ڵ�F.���˶�ʱ��Ϊt(��λ����)����FGΪһֱ�DZ�����������ֱ��������FGH����FGH��������ABCD�ص����ֵ����ΪS.
(1)��t��1.5ʱ��S��________����t��3ʱ��S��________.
(2)��DE��y1��AG��y2������ͼ��ʾ����������ϵ�У�����y1��y2����t�ĺ���ͼ����tΪ��ֵʱ���ı���DEGF��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����O��ֱ��Ϊ7��Բ��O��ֱ��l�ľ���Ϊ3����ֱ��l���O��λ�ù�ϵ�ǣ�������
A. ����B. ����C. �ཻD. ���л��ཻ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com