
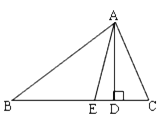
【题目】如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=40°,∠C=70°,求∠DAE的度数,并说明理由;
(2)若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系 .(不需说明理由)
【答案】(1)15°;(2)![]()
【解析】
(1)利用三角形的内角和定理求出∠BAC,再利用角平分线定义求∠BAD,最后求出∠DAE的度数,即可解答;
(2)根据三角形内角和等于180°,所以∠BAC=180°-∠B-∠C,因为AE平分∠BAC,利用∠BAD=90°-∠B,可得结论.
解:(1)∵∠C=70°,∠B=40°,
∴∠BAC=180°-(∠B+∠C)=180°-40°-70°=70°,
∵AE平分∠BAC,
∴∠CAE=![]() ∠BAC=35°
∠BAC=35°
∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=90°-70°=20°,
∴∠DAE=∠CAE-∠CAD=35°-20°=15°;
(2) ![]() ,
,
理由:∵AE为角平分线,
∴∠BAE=![]() ,
,
∵AD⊥BC,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAD-∠BAE
=90°-∠B-![]()
==![]()
=![]() .
.


科目:初中数学 来源: 题型:
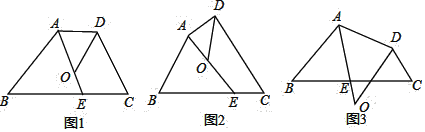
【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE= °;
②如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场11月初花费15 000元购进一批某品牌英语点读笔,因深受顾客喜爱,销售一空.该商场于12月初又花费24 000元购进一批同品牌英语点读笔,且所购数量是11月初的1.5倍,但每支进价涨了10元.
(1)求商场11月初购进英语点读笔多少支?
(2)11月份商场该品牌点读笔每支的售价是270元,若12月份购买的点读笔全部售完,且所获利润是11月份利润的1.2倍,求12月份该品牌点读笔每支的售价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上货物不超过5天卸货完毕,那么平均每天至少要缷货多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,﹣2),反比例函数![]() 的图象经过点C,一次函数
的图象经过点C,一次函数![]() 的图象经过A、C两点.
的图象经过A、C两点.

(1)求反比例函数与一次函数的解析式;
(2)求反比例函数与一次函数的另一个交点M的坐标;
(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
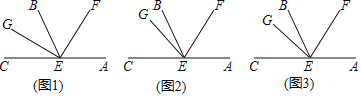
【题目】如图,E是直线AC上一点,EF是∠AEB的平分线.
(1)如图1,若EG是∠BEC的平分线,求∠GEF的度数;
(2)如图2,若GE在∠BEC内,且∠CEG=3∠BEG,∠GEF=75°,求∠BEG的度数.
(3)如图3,若GE在∠BEC内,且∠CEG=n∠BEG,∠GEF=α,求∠BEG(用含n、α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的函数关系式为![]() ,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,
,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,

(1)求直线l2的解析式;
(2)求△ADC的面积;
(3)在直线l2上存在一点F(不与C重合),使得△ADF和△ADC的面积相等,请求出F点的坐标;
(4)在x轴上是否存在一点E,使得△BCE的周长最短?若存在请求出E点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c在数轴上的位置如图所示,回答下列问题:
(1)化简:3|a﹣c|﹣2|﹣a﹣b|;
(2)令y=|x﹣a|+|x﹣b|+|x﹣c|,x满足什么条件时,y有最小值,求最小值
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com