
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
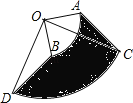
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
【答案】(1)将△AOC绕点O顺时针旋转90°可以得到△BOD;(2)![]() π(cm2).
π(cm2).
【解析】
试题分析:(1)根据旋转的定义求解;
(2)先利用弧长公式计算出OA=2,再根据旋转的性质得到△AOC≌△BOD,则S△AOC=S△BOD,接着根据S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分得到S阴影部分=S扇形COD﹣S扇形AOB,然后利用扇形的面积公式计算即可.
解:(1)∵扇形OAB和扇形OCD的圆心角都是90°,
∴OA=OB,OC=OD,∠AOB=∠COD=90°,
∴将△AOC绕点O顺时针旋转90°可以得到△BOD;
(2)∵![]() =π,
=π,
∴OA=2,
∵△AOC绕点O顺时针旋转90°可以得到△BOD,
∴△AOC≌△BOD,
∴S△AOC=S△BOD,
∵S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分,
∴S阴影部分=S扇形COD﹣S扇形AOB=![]() ﹣
﹣![]() =
=![]() π(cm2).
π(cm2).


科目:初中数学 来源: 题型:
【题目】阅读下文,寻找规律.
计算:(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4….
(1)观察上式,并猜想:(1﹣x)(1+x+x2+…+xn)= .
(2)根据你的猜想,计算:1+3+32+33…+3n= .(其中n是正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.

(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
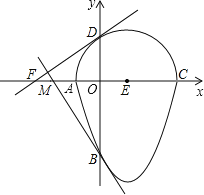
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
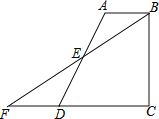
(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=ADAB;④ABCD=ADCB,能满足△ADC与△ACB相似的条件是( )

A.①、②、③ B.①、③、④ C.②、③、④ D.①、②、④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第六个正方形A6B6C6D6周长是 .
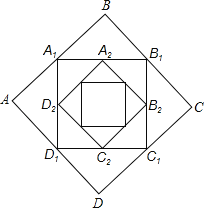
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬“东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com