
����Ŀ����ͼ�����ǰ�һ����Բ�������ߵ�һ����Χ�ɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ�����Բֻ��һ�����㣬������ֱ�߽�����Բ�����ߣ���֪A��B��C��D�ĵ�Ϊ��Բ��������Ľ��㣬EΪ��Բ��Բ�ģ������ߵĽ���ʽΪy=x2��2x��3��ACΪ��Բ��ֱ����
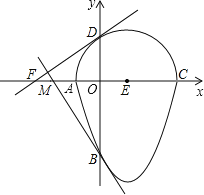
��1���ֱ����A��B��C��D�ĵ�����ꣻ
��2������D�Ĺ�Բ������DF�Ľ���ʽ��
��3����������B�Ĺ�Բ��������x�ύ�ڵ�M������OBM�������
���𰸡���1����0��![]() ������2��y=
������2��y=![]() x+
x+![]() ����3��
����3��![]() ��
��
��������
�����������1������DE�������������ϵ�������������A��B��C�����꣬�������������Բ��ֱ�������ݹ��ɶ������OD�ij����õ���D�����ꣻ
��2��������Ӱ�������EF�ij����õ���F�����꣬���ô���ϵ�������������D�Ĺ�Բ������DF�Ľ���ʽ��
��3���������ߵ����ʵõ�������B�Ĺ�Բ��������������ֻ��һ�������㣬����һԪ���η��̵��б�ʽ��������M�����꣬���������ε������ʽ���㼴�ɣ�
�⣺��1������DE��
��y=x2��2x��3��
��x=0ʱ��y=��3��
y=0ʱ��x1=��1��x2=3��
����A����������1��0������B��������0����3������C��������3��0����
��AC=4��
��AE=DE=2��
��OE=1��
��OD=![]() =
=![]() ��
��
��D���������0��![]() ����
����
��2����DF�ǹ�Բ�����ߣ�
��ED��DF����DO��EF��
��DE2=EOEF��
��EF=4����OF=3��
����F����������3��0����
�辭����D�Ĺ�Բ������DF�Ľ���ʽΪy=kx+b��
��![]() ��
��
���![]() ��
��
��������D�Ĺ�Բ������DF�Ľ���ʽΪy=![]() x+
x+![]() ��
��
��3���辭����B�Ĺ�Բ�����ߵĽ���ʽΪ��y=ax+c��
����B��������0����3����
��������B�Ĺ�Բ�����ߵĽ���ʽΪ��y=ax��3��
������ã�������![]() ֻ��һ���⣬
ֻ��һ���⣬
��һԪ���η���x2����a+2��x=0��������ȵ�ʵ������
��=��a+2��2��4��1��0=0��
���a=��2��
��������B�Ĺ�Բ�����ߵĽ���ʽΪ��y=��2x��3��
��y=0ʱ��x=��![]() ��
��
����M����������![]() ��0������OM=
��0������OM=![]() ��
��
���OBM�����=![]() ��OM��OB=
��OM��OB=![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D��E�ֱ��ڱ�BC��AC�ϣ�����AD��DE������1=��B=��C��
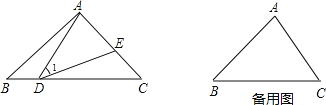
��1����������������д��������ȷ���ۣ���Ҫ��������������ĸ�����ߣ��ҽ��۹��������ӵ���ĸ�����߲��ܳ����ڽ����У�����֤����
�𣺽���һ�� ��
���۶��� ��
�������� ��
��2������B=45����BC=2������D��BC���˶�ʱ����D����B��C�غϣ���
����CE�����ֵ��
������ADE�ǵ��������Σ����ʱBD�ij���
��ע�⣺�ڵڣ�2�����������У��������ã�1���еó��Ľ��ۣ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O��Rt��ABC�����Բ����ACB=90����ACƽ����BAD��CD��AD��D��AD����O��E��
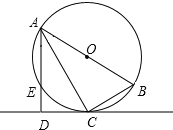
��1����֤��CDΪ��O�����ߣ�
��2������O��ֱ��Ϊ8cm��CD=2![]() cm������AE�ij���
cm������AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ�ĽǶ���90�������OAB������OCD������һ������AC��BD��
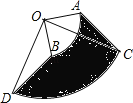
��1������AOC����������ͼ�α任���Եõ���BOD��
��2����![]() �ij�Ϊ��cm��OD=3cm����ͼ����Ӱ���ֵ�����Ƕ��٣�
�ij�Ϊ��cm��OD=3cm����ͼ����Ӱ���ֵ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=2x2+2����ƽ��1����λ�����������ߵĽ���ʽ�ǣ� ��
A��y=2x2+3
B��y=2x2+1
C��y=2��x+1��2+2
D��y=2��x��1��2+2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com