
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЕуDЁЂEЗжБ№дкБпBCЁЂACЩЯЃЌСЌНгADЁЂDEЃЌЧвЁЯ1=ЁЯB=ЁЯCЃЎ
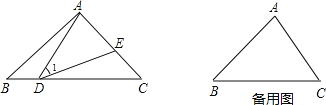
ЃЈ1ЃЉгЩЬтЩшЬѕМўЃЌЧыаДГіШ§Иіе§ШЗНсТлЃКЃЈвЊЧѓВЛдйЬэМгЦфЫћзжФИКЭИЈжњЯпЃЌевНсТлЙ§ГЬжаЬэМгЕФзжФИКЭИЈжњЯпВЛФмГіЯждкНсТлжаЃЌВЛБижЄУїЃЉ
Д№ЃКНсТлвЛЃК ЃЛ
НсТлЖўЃК ЃЛ
НсТлШ§ЃК ЃЎ
ЃЈ2ЃЉШєЁЯB=45ЁуЃЌBC=2ЃЌЕБЕуDдкBCЩЯдЫЖЏЪБЃЈЕуDВЛгыBЁЂCжиКЯЃЉЃЌ
ЂйЧѓCEЕФзюДѓжЕЃЛ
ЂкШєЁїADEЪЧЕШбќШ§НЧаЮЃЌЧѓДЫЪБBDЕФГЄЃЎ
ЃЈзЂвтЃКдкЕкЃЈ2ЃЉЕФЧѓНтЙ§ГЬжаЃЌШєгадЫгУЃЈ1ЃЉжаЕУГіЕФНсТлЃЌаыМгвджЄУїЃЉ
ЁОД№АИЁПЃЈ1ЃЉAB=ACЃЛЁЯAED=ЁЯADCЃЛЁїADEЁзЁїACDЃЛЃЈ2ЃЉЂй![]() ЃЛЂкЕБЁїADEЪЧЕШбќШ§НЧаЮЪБЃЌBDЕФГЄЮЊ1Лђ2Љ
ЃЛЂкЕБЁїADEЪЧЕШбќШ§НЧаЮЪБЃЌBDЕФГЄЮЊ1Лђ2Љ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЁЯB=ЁЯCЃЌИљОнЕШбќШ§НЧаЮЕФаджЪПЩЕУAB=ACЃЛгЩЁЯ1=ЁЯCЃЌЁЯAED=ЁЯEDC+ЁЯCЕУЕНЁЯAED=ЁЯADCЃЛгжгЩЁЯDAE=ЁЯCADЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈПЩЕУЕНЁїADEЁзЁїACDЃЛ
ЃЈ2ЃЉЂйгЩЁЯB=ЁЯCЃЌЁЯB=45ЁуПЩЕУЁїACBЮЊЕШбќжБНЧШ§НЧаЮЃЌдђAC=![]() BC=
BC=![]() ЁС2=
ЁС2=![]() ЃЌгЩЁЯ1=ЁЯCЃЌЁЯDAE=ЁЯCADЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈПЩЕУЁїADEЁзЁїACDЃЌдђгаADЃКAC=AEЃКADЃЌМДAD2=AEACЃЌ
ЃЌгЩЁЯ1=ЁЯCЃЌЁЯDAE=ЁЯCADЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈПЩЕУЁїADEЁзЁїACDЃЌдђгаADЃКAC=AEЃКADЃЌМДAD2=AEACЃЌ
AE=![]() =
=![]() =
=![]() AD2ЃЌЕБADЁЭBCЃЌADзюаЁЃЌЧвAD=
AD2ЃЌЕБADЁЭBCЃЌADзюаЁЃЌЧвAD=![]() BC=1ЃЌДЫЪБAEзюаЁЮЊ
BC=1ЃЌДЫЪБAEзюаЁЮЊ![]() ЃЌРћгУCE=ACЉAEЕУЕНCEЕФзюДѓжЕЃЛ
ЃЌРћгУCE=ACЉAEЕУЕНCEЕФзюДѓжЕЃЛ
ЂкЬжТлЃКЕБAD=AEЪБЃЌдђЁЯ1=ЁЯAED=45ЁуЃЌЕУЕНЁЯDAE=90ЁуЃЌдђЕуDгыBжиКЯЃЌВЛКЯЬтвтЩсШЅЃЛЕБEA=EDЪБЃЌШчЭМ1ЃЌдђЁЯEAD=ЁЯ1=45ЁуЃЌЫљвдгаADЦНЗжЁЯBACЃЌЕУЕНADДЙжБЦНЗжBCЃЌдђBD=1ЃЛ
ЕБDA=DEЪБЃЌШчЭМ2ЃЌгЩЁїADEЁзЁїACDЃЌвзЕУЁїCADЮЊЕШбќШ§НЧаЮЃЌдђDC=CA=![]() ЃЌгкЪЧгаBD=BCЉDC=2Љ
ЃЌгкЪЧгаBD=BCЉDC=2Љ![]() ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉAB=ACЃЛЁЯAED=ЁЯADCЃЛЁїADEЁзЁїACDЃЛ
ЃЈ2ЃЉЂйЁпЁЯB=ЁЯCЃЌЁЯB=45ЁуЃЌ
ЁрЁїACBЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAC=![]() BC=
BC=![]() ЁС2=
ЁС2=![]() ЃЌ
ЃЌ
ЁпЁЯ1=ЁЯCЃЌЁЯDAE=ЁЯCADЃЌ
ЁрЁїADEЁзЁїACDЃЌ
ЁрADЃКAC=AEЃКADЃЌМДAD2=AEACЃЌ
ЁрAE=![]() =
=![]() =
=![]() AD2ЃЌ
AD2ЃЌ
ЕБADзюаЁЪБЃЌAEзюаЁЃЌДЫЪБADЁЭBCЃЌAD=![]() BC=1ЃЌ
BC=1ЃЌ
ЁрAEЕФзюаЁжЕЮЊ![]() ЁС12=
ЁС12=![]() ЃЌ
ЃЌ
ЁрCEЕФзюДѓжЕ=![]() Љ
Љ![]() =
=![]() ЃЛ
ЃЛ
ЂкЕБAD=AEЪБЃЌ
ЁрЁЯ1=ЁЯAED=45ЁуЃЌ
ЁрЁЯDAE=90ЁуЃЌ
ЁрЕуDгыBжиКЯЃЌВЛКЯЬтвтЩсШЅЃЛ
ЕБEA=EDЪБЃЌШчЭМ1ЃЌ
ЁрЁЯEAD=ЁЯ1=45ЁуЃЌ
ЁрADЦНЗжЁЯBACЃЌ
ЁрADДЙжБЦНЗжBCЃЌ
ЁрBD=1ЃЛ
ЕБDA=DEЪБЃЌШчЭМ2ЃЌ
ЁпЁїADEЁзЁїACDЃЌ
ЁрDAЃКAC=DEЃКDCЃЌ
ЁрDC=CA=![]() ЃЌ
ЃЌ
ЁрBD=BCЉDC=2Љ![]() ЃЌ
ЃЌ
ЁрзлЩЯЫљЪіЃЌЕБЁїADEЪЧЕШбќШ§НЧаЮЪБЃЌBDЕФГЄЮЊ1Лђ2Љ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌAB=AC=6cmЃЌЁЯB=ЁЯCЃЌBC=4cmЃЌЕуDЮЊABЕФжаЕуЃЎ
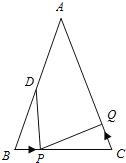
ЃЈ1ЃЉШчЙћЕуPдкЯпЖЮBCЩЯвд1cm/sЕФЫйЖШгЩЕуBЯђЕуCдЫЖЏЃЌЭЌЪБЃЌЕуQдкЯпЖЮCAЩЯгЩЕуCЯђЕуAдЫЖЏЃЎ
ЂйШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШЯрЕШЃЌОЙ§1УыКѓЃЌЁїBPDгыЁїCQPЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЛ
ЂкШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШВЛЯрЕШЃЌЕБЕуQЕФдЫЖЏЫйЖШЮЊЖрЩйЪБЃЌФмЙЛЪЙЁїBPDгыЁїCQPШЋЕШЃП
ЃЈ2ЃЉШєЕуQвдЂкжаЕФдЫЖЏЫйЖШДгЕуCГіЗЂЃЌЕуPвддРДЕФдЫЖЏЫйЖШДгЕуBЭЌЪБГіЗЂЃЌЖМФцЪБеыбиЁїABCШ§БпдЫЖЏЃЌдђОЙ§ КѓЃЌЕуPгыЕуQЕквЛДЮдкЁїABCЕФ БпЩЯЯргіЃПЃЈдкКсЯпЩЯжБНгаДГіД№АИЃЌВЛБиЪщаДНтЬтЙ§ГЬЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТЮФЃЌбАевЙцТЩЃЎ
МЦЫуЃКЃЈ1ЉxЃЉЃЈ1+xЃЉ=1Љx2ЃЌЃЈ1ЉxЃЉЃЈ1+x+x2ЃЉ=1Љx3ЃЌЃЈ1ЉxЃЉЃЈ1+x+x2+x3ЃЉ=1Љx4ЁЃЎ
ЃЈ1ЃЉЙлВьЩЯЪНЃЌВЂВТЯыЃКЃЈ1ЉxЃЉЃЈ1+x+x2+Ё+xnЃЉ= ЃЎ
ЃЈ2ЃЉИљОнФуЕФВТЯыЃЌМЦЫуЃК1+3+32+33Ё+3n= ЃЎЃЈЦфжаnЪЧе§ећЪ§ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЯТСаИїзщжаЃЌБэЪОЛЅЮЊЯрЗДвтвхЕФСПЪЧЃЈЁЁЁЁЃЉ
A. ЩЯЩ§гыЯТНЕ
B. РКЧђБШШќЪЄ5ГЁгыИК5ГЁ
C. ЯђЖЋзп3УзЃЌдйЯђФЯзп3Уз
D. діВњ10ЖжСИЪГгыМѕВњЉ10ЖжСИЪГ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯТСаУќЬтЃКЂйШєaЃО0ЃЌbЃО0ЃЌдђaЃЋbЃО0ЃЛЂкШєaЁйbЃЌдђa2Ёйb2ЃЛЂлСНЕужЎМфЃЌЯпЖЮзюЖЬЃЛЂмЭЌЮЛНЧЯрЕШЃЌСНжБЯпЦНааЃЎЦфжаецУќЬтЕФИіЪ§ЪЧ( )
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉЃЎ
A. ЦЕЪ§дНаЁЃЌЦЕТЪдНДѓ B. ЦЕЪ§ДѓЃЌЦЕТЪвВвЛЖЈДѓ
C. ЦЕЪ§вЛЖЈЪБЃЌЦЕТЪдНаЁЃЌзмДЮЪ§дНДѓ D. ЦЕЪ§КмДѓЪБЃЌЦЕТЪПЩФмГЌЙ§1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋГЄЗНаЮABCDбизХЖдНЧЯпBDелЕўЃЌЪЙЕуCТфдкCЁфДІЃЌBCЁфНЛADгкЕуEЃЎ

ЃЈ1ЃЉЪдХаЖЯЁїBDEЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєAB=4ЃЌAD=8ЃЌЧѓЁїBDEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮвУЧАбвЛИіАыдВгыХзЮяЯпЕФвЛВПЗжЮЇГЩЕФЗтБеЭМаЮГЦЮЊЁАЙћдВЁБЃЎШчЙћвЛЬѕжБЯпгыЙћдВжЛгавЛИіНЛЕуЃЌдђетЬѕжБЯпНазіЙћдВЕФЧаЯпЃЎвбжЊAЁЂBЁЂCЁЂDЫФЕуЮЊЙћдВгызјБъжсЕФНЛЕуЃЌEЮЊАыдВЕФдВаФЃЌХзЮяЯпЕФНтЮіЪНЮЊy=x2Љ2xЉ3ЃЌACЮЊАыдВЕФжБОЖЃЎ
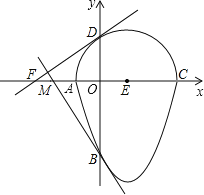
ЃЈ1ЃЉЗжБ№ЧѓГіAЁЂBЁЂCЁЂDЫФЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓОЙ§ЕуDЕФЙћдВЕФЧаЯпDFЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШєОЙ§ЕуBЕФЙћдВЕФЧаЯпгыxжсНЛгкЕуMЃЌЧѓЁїOBMЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
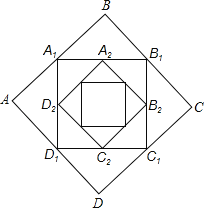
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌЫГДЮСЌНге§ЗНаЮABCDЫФБпЕФжаЕуЕУЕНЕквЛИіе§ЗНаЮA1B1C1D1ЃЌгЩЫГДЮСЌНге§ЗНаЮA1B1C1D1ЫФБпЕФжаЕуЕУЕНЕкЖўИіе§ЗНаЮA2B2C2D2ЁЃЌвдДЫРрЭЦЃЌдђЕкСљИіе§ЗНаЮA6B6C6D6жмГЄЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com