
【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
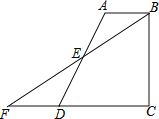
(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
【答案】(1)平行四边形,理由见解析(2)25
【解析】
试题分析:(1)由平行线的性质得出内错角相等,由中点的定义得出AE=DE,由ASA证明△ABE≌△DFE,得出BE=FE,即可得出结论;
(2)由(1)可知△ABE≌△DFE,所以求△BCF的面积可转化为求梯形ABCD的面积,根据梯形的面积公式计算即可.
解:(1)如图所示:
四边形ABDF是平行四边形,理由如下:
∵AB∥CD,
∴∠A=∠EDF,
∵E是AD的中点,
∴AE=DE,
在△ABE和△DFE中, ,
,
∴△ABE≌△DFE(ASA),
∴BE=FE,
∴四边形ABDF是平行四边形;
(2)∵△ABE≌△DFE,BC⊥CD,
∴△BCF的面积=梯形ABCD的面积=![]() (AB+CD)×BC=
(AB+CD)×BC=![]() (4+6)×5=25.
(4+6)×5=25.



 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,AB=AC,CE平分∠ACB交AB于点E.
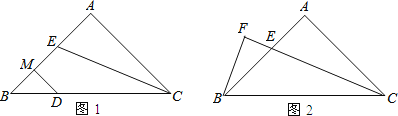
(1)∠B= 度.
(2)如图1,若点D在斜边BC上,DM垂直平分BE,垂足为M.求证:BD=AE;
(3)如图2,过点B作BF⊥CE,交CE的延长线与点F.若CE=6,求△BEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.
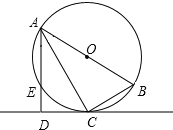
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2![]() cm,求弦AE的长.
cm,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
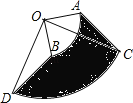
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题是( )
A. 同位角相等 B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角 D. 在同一平面内,如果a∥b,b∥c,则a∥c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.

(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)设方程两根为x1,x2是否存在实数a,使![]() ?若存在求出实数a,若不存在,请说明理由.
?若存在求出实数a,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com