
【题目】已知,在△ABC中,∠BAC=90°,AB=AC,CE平分∠ACB交AB于点E.
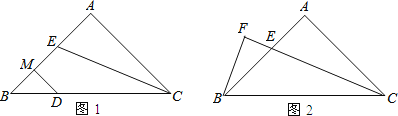
(1)∠B= 度.
(2)如图1,若点D在斜边BC上,DM垂直平分BE,垂足为M.求证:BD=AE;
(3)如图2,过点B作BF⊥CE,交CE的延长线与点F.若CE=6,求△BEC的面积.
【答案】(1)45;(2)见解析;(3)9.
【解析】
试题分析:(1)根据等腰直角三角形的性质解答即可;
(2)连接DE,由∠BAC=90°,AB=AC,可得∠B=45°,由DM垂直平分BE,可得BD=DE,进而判断△BDE是等腰直角三角形,所以ED⊥BD,然后由角平分线的性质可得ED=AE,根据等量代换可得BD=AE;
(3)延长BF,CA,交与点G,由CE平分∠ACB,可得∠ACE=∠BCE,由BF⊥CE,可得∠BFC=∠GFC=90°,然后由三角形内角和定理可得:∠GBC=∠G,进而可得BC=GC,然后由等腰三角形的三线合一,可得BF=FG=![]() BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
解:(1)∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=45°,
故答案为:45;
(2)连接ED,如图1,
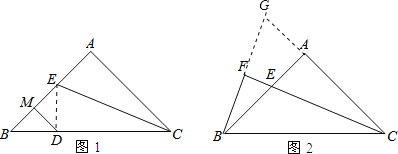
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵DM垂直平分BE,
∴BD=ED,
∴∠BED=∠B=45°,
∴∠EDC=∠B+∠BED=90°,
∵CE平分∠ACB,∠BAC=90°,∠EDC=90°,
∴ED=EA,
∴BD=AE;
(3)延长BF和CA交于点G,如图2,
∵CE平分∠ACB,
∴∠ACF=∠BCF,
∵BF⊥CE,
∴∠BFC=∠GFC=90°,
∴∠CBG=∠CGB,
∴CG=CB,
∴BF=GF=![]() BG,
BG,
∵∠GFC=∠GAB=90°,
∴∠ACF+∠G=90°,
∴∠ABG+∠G=90°,
∴∠ACF=∠ABG,
在△ACE和△ABG中
∠ACE=∠ABG
AC=AB
∠EAC=∠GAB
∴△ACE≌△ABG(ASA),
∴CE=BG,
∴CE=2BF,
∵CE=6,
∴BF=![]() CE=3,
CE=3,
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题:①相等的两个角是对顶角;②若∠1+∠2=180°,则∠1与∠2互为补角;③同旁内角互补;④垂线段最短;⑤同角或等角的余角相等;⑥经过直线外一点,有且只有一条直线与这条直线平行,其中假命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算结果正确的是( )
A.(6ab2﹣4a2b)3ab=18ab2﹣12a2b
B.(﹣x)(2x+x2﹣1)=﹣x3﹣2x2+1
C.(﹣3x2y)(﹣2xy+3yz﹣1)=6x3y2﹣9x2y2z2+3x2y
D.(![]() a3﹣
a3﹣![]() b)2ab=
b)2ab=![]() a4b﹣ab2
a4b﹣ab2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
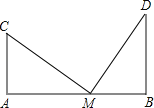
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下文,寻找规律.
计算:(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4….
(1)观察上式,并猜想:(1﹣x)(1+x+x2+…+xn)= .
(2)根据你的猜想,计算:1+3+32+33…+3n= .(其中n是正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列各组中,表示互为相反意义的量是( )
A. 上升与下降
B. 篮球比赛胜5场与负5场
C. 向东走3米,再向南走3米
D. 增产10吨粮食与减产﹣10吨粮食
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( ).
A. 频数越小,频率越大 B. 频数大,频率也一定大
C. 频数一定时,频率越小,总次数越大 D. 频数很大时,频率可能超过1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
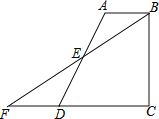
(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com