
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.
(1)若点C′刚好落在对角线BD上时,BC′=;
(2)若点C′刚好落在线段AB的垂直平分线上时,求CE的长;
(3)若点C′刚好落在线段AD的垂直平分线上时,求CE的长.
【答案】
(1)4
(2)
解:如图2,连接CC′,
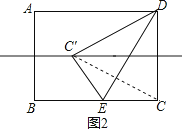
∵点C′在AB的垂直平分线上,
∴点C′在DC的垂直平分线上,
∴CC′=DC′=DC,则△DC′C是等边三角形,
设CE=x,易得DE=2x,
由勾股定理得:(2x)2﹣x2=62,
解得:x=2 ![]() ,
,
即CE的长为2 ![]() ;
;
(3)
解:作AD的垂直平分线,交AD于点M,交BC于点N,分两种情况讨论:
①当点C′在矩形内部时,如图3,
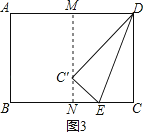
∵点C′在AD的垂直平分线上,
∴DM=4,
∵DC′=6,
由勾股定理得:MC′=2 ![]() ,∴NC′=6﹣2
,∴NC′=6﹣2 ![]() ,
,
设EC=y,则C′E=y,NE=4﹣y,
故NC′2+NE2=C′E2,
即(6﹣2)2+(4﹣y)2=y2,
解得:y=9﹣3 ![]() ,即CE=9﹣3
,即CE=9﹣3 ![]() ;
;
②当点C′在矩形外部时,如图4,
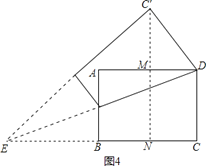
∵点C′在AD的垂直平分线上,
∴DM=4,
∵DC′=6,
由勾股定理得:MC′=2 ![]() ,∴NC′=6+2
,∴NC′=6+2 ![]() ,
,
设EC=z,则C′E=a,NE=z﹣4
故NC′2+NE2=C′E2,
即(6+2 ![]() )2+(z﹣4)2=z2,解得:z=9+3
)2+(z﹣4)2=z2,解得:z=9+3 ![]() ,即CE=9+3
,即CE=9+3 ![]() ,综上所述:CE的长为9±3
,综上所述:CE的长为9±3 ![]() .
.
【解析】解:如图1,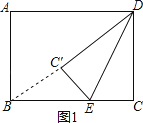
∵点B,C′,D在同一直线上,
∴BC′=BD﹣DC′=BD﹣DC=10﹣6=4;
故答案为:4;
(1)根据点B,C′,D在同一直线上得出BC′=BD﹣DC′=BD﹣DC求出即可;(2)利用垂直平分线的性质得出CC′=DC′=DC,则△DC′C是等边三角形,进而利用勾股定理得出答案;(3)利用①当点C′在矩形内部时,②当点C′在矩形外部时,分别求出即可.


科目:初中数学 来源: 题型:
【题目】如图所示,小明家小区空地上有两颗笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=30°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点在一条直线上,求树EF的高度.(![]() ≈1.7,
≈1.7,![]() ≈1.4,结果保留一位小数)
≈1.4,结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电缆在空中架设时,两端挂起的电缆下垂都近似抛物线y= ![]() x2的形状.今在一个坡度为1:5的斜坡上,沿水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱(如图),这种情况下在竖直方向上,下垂的电缆与地面的最近距离为( )
x2的形状.今在一个坡度为1:5的斜坡上,沿水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱(如图),这种情况下在竖直方向上,下垂的电缆与地面的最近距离为( ) 
A.12.75米
B.13.75米
C.14.75米
D.17.75米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计,结果保留根号形式)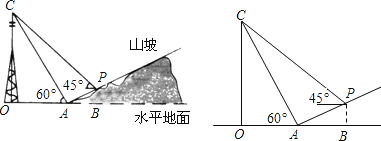
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】育才中学计划召开“诚信在我心中”主题教育活动,需要选拔活动主持人,经过全校学生投票推荐,有2名男生和1名女生被推荐为候选主持人.
(1)小明认为,如果从3名候选主持人中随机选拔1名主持人,不是男生就是女生,因此选出的主持人是男生和女生的可能性相同,你同意他的说法吗?为什么?
(2)如果从3名候选主持人中随机选拔2名主持人,请通过列表或树状图求选拔出的2名主持人恰好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设四棱锥P﹣ABCD的底面不是平行四边形,用平面 α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α( ) 
A.不存在
B.只有1个
C.恰有4个
D.有无数多个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com