
【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图1,在矩形纸片ABCD和矩形纸片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,点E是AD的中点,矩形纸片EFGH以点E为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图1,当EF与AB相交于点M,EH与BC相交于点N时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当AM=CN时,AM与BM有怎样的数量关系,说明理由.
(3)“创新”小组提出的问题是;若矩形EFGH继续以点E为旋转中心进行逆时针旋转,当∠AEF=60°时,请你在图2中画出旋转后的示意图,并求出此时EF将边BC分成的两条线段的长度.
【答案】
(1)
解:如图1,过点E作EP⊥BC,垂足为点P,

则四边形ABPE是矩形,
∴PE=AB=1,∠AEP=90°,
∵点E是AD的中点,
∴AE=DE= ![]() AD=1,
AD=1,
∴PE=AE,
∵∠MEN=∠AEP=90°,
∴∠MEN﹣∠MEP=∠AEP﹣∠MEP,
∴∠PEN=∠AEM,
∵PE=AE,∠EPN=∠EAM=90°,
∴△PEN≌△AEM,
∴EM=EN
(2)
解:由(1)知,△PEN≌△AEM,
∴AM=PN,
∵AM=CN,
∴PN=CN= ![]() PC,
PC,
∵四边形EPCD是矩形,
∴PC=DE=1,PN=CN= ![]() ,
,
∴AM=PN= ![]() ,BM=AB﹣AM=
,BM=AB﹣AM= ![]() ,
,
∴AM=BM
(3)
解:如图2,
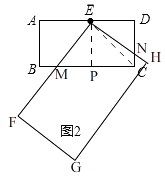
当∠AEF=60°时,
设EF与BC交于M,EH与CD交于N,过点E作EP⊥BC于P,连接EC,
由(1)知,CP=EP=1,AD∥BC,
∴∠EMP=∠AEF=60°,
在Rt△PEM中,PM= ![]() =
= ![]() ,
,
∴BM=BP﹣PM=1﹣ ![]() ,CM=PC+PM=1+
,CM=PC+PM=1+ ![]() ,
,
∴EF将边BC分成的两条线段的长度为1﹣ ![]() ,1+
,1+ ![]() .
.
【解析】(1)先判断出PE=AE,再判断出∠PEN=∠AEM,进而得到△PEN≌△AEM,即可得出结论;(2)先判断出PN=CN= ![]() PC,进而求出PN=CN=
PC,进而求出PN=CN= ![]() ,再判断出AM=PN,即可得出BM=
,再判断出AM=PN,即可得出BM= ![]() ,结论得证;(3)在直角三角形PEM中,求出PM,再用线段的和差即可得出结论.
,结论得证;(3)在直角三角形PEM中,求出PM,再用线段的和差即可得出结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G. 
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.
(1)点P(a,b)经过T变换后得到的点Q的坐标为 ![]() ;若点M经过T变换后得到点N(6,﹣
;若点M经过T变换后得到点N(6,﹣ ![]() ),则点M的坐标为
),则点M的坐标为 ![]() .
.
(2)A是函数y= ![]() x图象上异于原点O的任意一点,经过T变换后得到点B.
x图象上异于原点O的任意一点,经过T变换后得到点B.
①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求△OAB的面积与△OAD的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京市2009﹣2014年轨道交通日均客运量统计如图所示.根据统计图中提供的信息,预估2015年北京市轨道交通日均客运量约 万人次,你的预估理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
(1)求m的值
(2)若PA=2AB,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.
(1)若点P在线段CD上,如图1.
①依题意补全图1;
②判断AH与PH的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康,太原市会持续出现雾霾天气吗?在2016年2月周末休息期间,某校九年级1班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察并回答下列问题:
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |
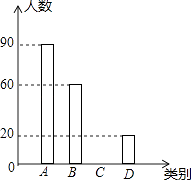
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若太原市有300万人口,请你估计持有A,B两类看法的市民共有多少人?
(3)学校要求小颖同学在A,B,C,D这四个雾霾天气的主要成因中,随机抽取两项作为课题研究的项目进行考察分析,请用画树状图或列表的方法,求出小颖同学刚好抽到B(汽车尾气排放),C(城中村燃煤问题)的概率.(用A,B,C,D表示各项目)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.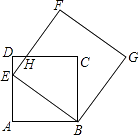
(1)当E为边AD的中点时,求DH的长;
(2)当tan∠ABE= ![]() 时,连接CF,求CF的长;
时,连接CF,求CF的长;
(3)连接CE,求△CEF面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com