
【题目】操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.
(1)点P(a,b)经过T变换后得到的点Q的坐标为 ![]() ;若点M经过T变换后得到点N(6,﹣
;若点M经过T变换后得到点N(6,﹣ ![]() ),则点M的坐标为
),则点M的坐标为 ![]() .
.
(2)A是函数y= ![]() x图象上异于原点O的任意一点,经过T变换后得到点B.
x图象上异于原点O的任意一点,经过T变换后得到点B.
①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求△OAB的面积与△OAD的面积之比.
【答案】
(1)
如图1,连接CQ,过Q作QD⊥PC于点D,
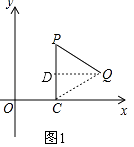
由旋转的性质可得PC=PQ,且∠CPQ=60°,
∴△PCQ为等边三角形,
∵P(a,b),
∴OC=a,PC=b,
∴CD= ![]() PC=
PC= ![]() b,DQ=
b,DQ= ![]() PQ=
PQ= ![]() b,
b,
∴Q(a+ ![]() b,
b, ![]() b);
b);
设M(x,y),则N点坐标为(x+ ![]() y,
y, ![]() y),
y),
∵N(6,﹣ ![]() ),
),
∴ 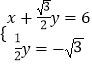 ,解得
,解得 ![]() ,
,
∴M(9,﹣2 ![]() );
);
故答案为:(a+ ![]() b,
b, ![]() b);(9,﹣2
b);(9,﹣2 ![]() )
)
(2)
①∵A是函数y= ![]() x图象上异于原点O的任意一点,
x图象上异于原点O的任意一点,
∴可取A(2, ![]() ),
),
∴2+ ![]() ×
× ![]() =
= ![]() ,
, ![]() ×
× ![]() =
= ![]() ,
,
∴B( ![]() ,
, ![]() ),
),
设直线OB的函数表达式为y=kx,则 ![]() k=
k= ![]() ,解得k=
,解得k= ![]() ,
,
∴直线OB的函数表达式为y= ![]() x;
x;
②设直线AB解析式为y=k′x+b,
把A、B坐标代入可得 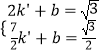 ,解得
,解得 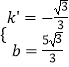 ,
,
∴直线AB解析式为y=﹣ ![]() x+
x+ ![]() ,
,
∴D(0, ![]() ),且A(2,
),且A(2, ![]() ),B(
),B( ![]() ,
, ![]() ),
),
∴AB= ![]() =
= ![]() ,AD=
,AD= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
【解析】(1)连接CQ可知△PCQ为等边三角形,过Q作QD⊥PC,利用等边三角形的性质可求得CD和QD的长,则可求得Q点坐标;设出M点的坐标,利用P、Q坐标之间的关系可得到点M的方程,可求得M点的坐标;(2)①可取A(2, ![]() ),利用T变换可求得B点坐标,利用待定系数示可求得直线OB的函数表达式;②由待定系数示可求得直线AB的解析式,可求得D点坐标,则可求得AB、AD的长,可求得△OAB的面积与△OAD的面积之比.
),利用T变换可求得B点坐标,利用待定系数示可求得直线OB的函数表达式;②由待定系数示可求得直线AB的解析式,可求得D点坐标,则可求得AB、AD的长,可求得△OAB的面积与△OAD的面积之比.
【考点精析】本题主要考查了一次函数的性质和一次函数的图象和性质的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.


科目:初中数学 来源: 题型:
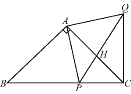
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形?若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上什么位置时,△ACQ是等腰三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,我们把,每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,在下列如图所示的正方形网格中,每个小正方形的边长为1. 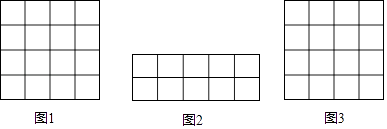
(1)请你在图1中画一个格点图形,且该图形是边长为 ![]() 的菱形;
的菱形;
(2)请你在图2中用网格线段将其切割成若干个三角形和正方形,拼接成一个与其面积相等的正方形,并在图3中画出格点正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.
《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”
设每头牛值金x两,每只羊值金y两,可列方程组为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图1,在矩形纸片ABCD和矩形纸片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,点E是AD的中点,矩形纸片EFGH以点E为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图1,当EF与AB相交于点M,EH与BC相交于点N时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当AM=CN时,AM与BM有怎样的数量关系,说明理由.
(3)“创新”小组提出的问题是;若矩形EFGH继续以点E为旋转中心进行逆时针旋转,当∠AEF=60°时,请你在图2中画出旋转后的示意图,并求出此时EF将边BC分成的两条线段的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果10b=n,那么称b为n的劳格数,记为b= d(n).
(1)根据劳格数的定义,可知d(10)=1,d(102)=2,直接写出 d(103)的值.
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)= d(m)+ d(n);d(![]() )= d(m)- d(n).
)= d(m)- d(n).
根据运算性质,求:![]() ,若
,若 ![]() ,直接写出
,直接写出![]() ,
,![]() 的值.
的值.
(3)下表中与数x对应的劳格数 ![]() 有且只有两个是错误的,请找出错误的劳格数并改正.
有且只有两个是错误的,请找出错误的劳格数并改正.
| 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com