

分析 (1)根据题中所给的奇异三角形的定义直接进行判断即可;
(2)分2$\sqrt{2}$是斜边和直角边两种情况讨论,再根据勾股定理判断出所给的三角形是否符合奇异三角形的定义;(3)结合(2)提出问题即可.
解答 解:(1)①设等边三角形的一边为a,则a2+a2=2a2,
∴符合“奇异三角形”的定义.
∴“等边三角形一定是奇异三角形”,正确;
故答案为:是;
②∵12+($\sqrt{7}$)2=8=2×22,
∴若某三角形的三边长分别为1、$\sqrt{7}$、2,则该三角形是奇异三角形;
故答案为:是;
(2)分两种情况:
①当2$\sqrt{2}$为斜边时,第三边长=$\sqrt{(2\sqrt{2})^{2}-{2}^{2}}$=2,
∵22+(2$\sqrt{2}$)2≠2×22,
∴不是奇异三角形;
②当2$\sqrt{2}$为直角边长时,第三边长=$\sqrt{{2}^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{3}$,
∵22+(2$\sqrt{3}$)2=2×(2$\sqrt{2}$)2,
∴是奇异三角形;
直角三角形的三边之比为2:2$\sqrt{2}$:2$\sqrt{3}$=1:$\sqrt{2}$:$\sqrt{3}$;
故答案为:2$\sqrt{3}$,1:$\sqrt{2}$:$\sqrt{3}$;
(3)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,a:b:c的比是多少.
点评 本题考查的是奇异三角形的定义、勾股定理的应用,在解答(2)时要注意分类讨论是解题关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x≠-4 | B. | x≥-3 | C. | x≥-3或x≠-4 | D. | x>-3且x≠-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
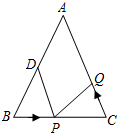 如图,已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
如图,已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$不是分数,$\frac{π}{2}$是无理数 | |
| B. | 无理数包括正无理数、0和负无理数 | |
| C. | (1-x)2的平方根是x-1和1-x | |
| D. | 数轴上的点和所有的实数是一一对应的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com