杨梅开始采摘啦！每筐杨梅以5千克为基准，超过的千克数记为正数，不足的千克数记为负数，记录如图，则这4筐杨梅的总质量是
A. 19.7千克 B. 19.9千克 C. 20.1千克 D. 20.3千克
科目：初中数学 来源：2014年初中毕业升学考试（浙江宁波卷）数学（解析版） 题型：填空题
一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中，未被小正方形覆盖部分的面积是 （用
，
的代数式表示）
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（浙江宁波卷）数学（解析版） 题型：选择题
已知命题“关于
的一元二次方程
，当
时必有实数解”，能说明这个命题是假命题的一个反例是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（江西南昌卷）数学（解析版） 题型：解答题
如图1，边长为4的正方形ABCD中，点E在AB边上（不与点A，B重合），点F在BC边上（不与点B，C重合）．
第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G；
第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；
依次操作下去…
（1）图2中的△EFD是经过两次操作后得到的，其形状为 ，求此时线段EF的长；
（2）若经过三次操作可得到四边形EFGH．
①请判断四边形EFGH的形状为 ，此时AE与BF的数量关系是 ；
②以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x的函数关系式及面积y的取值范围；
（3）若经过多次操作可得到首尾顺次相接的多边形，其最大边数是多少？它可能是正多边形吗？如果是，请直接写出其边长；如果不是，请说明理由．
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（江苏镇江卷）数学（解析版） 题型：解答题
我们知道平行四边形有很多性质.
现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.
【发现与证明】
ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连结B′D.
结论1：B′D∥AC；
结论2：△AB′C与ABCD重叠部分的图形是等腰三角形.
……
请利用图1证明结论1或结论2（只需证明一个结论）.
【应用与探究】在ABCD中，已知∠B=30°，将△ABC沿AC翻折至△AB′C，连结B′D.
（1）如图1，若
，则∠ACB= °，BC= ；
（2）如图2，
，BC=1，AB′与边CD相交于点E，求△AEC的面积；
（3）已知，当BC长为多少时，是△AB′D直角三角形？
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（江苏连云港卷）数学（解析版） 题型：填空题
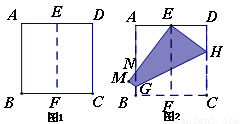
如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF，如图2，展形再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为M，EM交AB于N，则tan∠ANE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
