Question

我们知道平行四边形有很多性质.

现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.

【发现与证明】ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连结B′D.

结论1：B′D∥AC；

结论2：△AB′C与ABCD重叠部分的图形是等腰三角形.

……

请利用图1证明结论1或结论2（只需证明一个结论）.

【应用与探究】在ABCD中，已知∠B=30°，将△ABC沿AC翻折至△AB′C，连结B′D.

（1）如图1，若，则∠ACB= °，BC= ；

（2）如图2，，BC=1，AB′与边CD相交于点E，求△AEC的面积；

（3）已知，当BC长为多少时，是△AB′D直角三角形？

 

 

Answer 1

【发现与证明】证明见解析；【应用与探究】(1) 45，；（2）；（3）6,2, 4或3.

【解析】

试题分析：【发现与证明】根据翻折对称的性质,平行四边形的性质和三角形内角和定理可得证.

【应用与探究】(1)∵△ABC沿AC翻折至△AB′C，∠B=30°，∴∠AB′C=∠B=30°.

∵，∴∠CB′D=45°.

由【发现与证明】的结论,B′D∥AC,

∴∠ACB=∠ACB′=∠C B′D=45°.

如答图7,过A点作AP⊥BC于点P,

∵∠B=30°，,

∴.

∵∠ACB=45°,∴.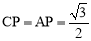

∴.

(2)过C点分别作CG⊥AB，CH⊥A B′，垂足分别为G、H,应用含30度直角三角形的性质和勾股定理AE和CH的长即可求出△AEC的面积.

(3)分∠B′AD=90°, ∠AB′D=90°和∠ADB′=90°三种情况讨论即可.

试题解析：【解析】
【发现与证明】证明：如答图1，设AD与B′C相交于点F，

∵△ABC沿AC翻折至△AB′C，

∴△ABC≌△△AB′C，∠ACB=∠ACB′，BC= B′C.

∵四边形ABCD是平行四边形，

∴AD=BC，AD∥BC.

∴B′C=AD，∠ACB=∠CAD.

∴.∴AF=CF.

∴B′F=DF.

∴.

∵∠AFC=∠B′FD，∴.∴B′D∥AC.

【应用与探究】

（1）45，.

（2）如答图2，过C点分别作CG⊥AB，CH⊥AB′，垂足分别为G、H.

∴CG=CH.

在Rt△BCG中，∠BGC=90°，BC=1，∠B=30°，

∴.

∵，∴.

∵△AGC≌△AHC,∴.

设AE=CE=x,

由勾股定理得,,即,解得.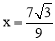

∴△AEC的面积.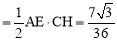

（3）按△AB′D中的直角分类:

①当∠B′AD=90°时,如答图3,

∵∠B′DA=∠DAC=∠B=30°,AB′=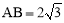,∴BC=AD=6.

如答图4,

∵∠A B′D=∠B=30°,AB′=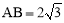,∴BC=AD=2.

②当∠AB′D=90°时,如答图5,

∵∠B′AD=∠B=30°,AB′=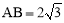,∴BC=AD=4.

③当∠ADB′=90°时,如答图6,

∵∠DAB′=∠A B′C=∠B=30°,AB′=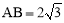,∴BC=AD=3.

综上所述, 当BC长为6,2, 4或3时，是△AB′D直角三角形.

考点：1. 翻折问题；2.平行四边形的性质；3.翻折对称的性质；4.全等三角形的判定和性质；5.三角形内角和定理；6.等腰三角形的判定和性质；7.勾股定理；8. 含30度直角三角形的性质；9.分类思想的应用.