
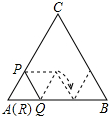
 如图,正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为2π cm.(结果保留π)
如图,正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为2π cm.(结果保留π) 科目:初中数学 来源: 题型:填空题
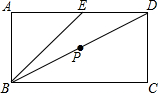 如图,矩形ABCD中,AB=1,AD=2,E是AD中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于$\sqrt{2}$或$\frac{\sqrt{5}}{3}$或$\frac{6\sqrt{5}}{5}$.
如图,矩形ABCD中,AB=1,AD=2,E是AD中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于$\sqrt{2}$或$\frac{\sqrt{5}}{3}$或$\frac{6\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 每天早晨某校八年级(1)班学生起床的时间 | |
| B. | 某校八年级学生对数学课的喜爱程度 | |
| C. | 某栋家属楼的居民所喜欢的汽车颜色 | |
| D. | 某市全部汽车在春节期间所排放尾气的体积 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com