
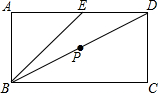
 如图,矩形ABCD中,AB=1,AD=2,E是AD中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于$\sqrt{2}$或$\frac{\sqrt{5}}{3}$或$\frac{6\sqrt{5}}{5}$.
如图,矩形ABCD中,AB=1,AD=2,E是AD中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于$\sqrt{2}$或$\frac{\sqrt{5}}{3}$或$\frac{6\sqrt{5}}{5}$. 分析 先根据矩形的性质及中点的定义得出∠BAD=90°,AE=DE=1,那么△ABE是等腰直角三角形,BE=$\sqrt{2}$AB=$\sqrt{2}$.再分三种情况讨论:①BP=BE;②PB=PE;③EB=EP.
解答 解:∵矩形ABCD中,AB=1,AD=2,E是AD中点,
∴∠BAD=90°,AE=DE=1,
∴△ABE是等腰直角三角形,
∴BE=$\sqrt{2}$AB=$\sqrt{2}$.
若△BEP为等腰三角形,则分三种情况:
①当BP=BE时,显然BP=$\sqrt{2}$;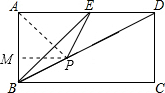 ②当PB=PE时,如图,连结AP.
②当PB=PE时,如图,连结AP.
∵PB=PE,AB=AE,
∴AP垂直平分BE,
∵△ABE是等腰直角三角形,
∴∠BAP=∠EAP=45°.
作PM⊥AB于M,设PM=x,
∵S△ABD=S△ABP+S△APD
∴$\frac{1}{2}$×1•x+$\frac{1}{2}$×2•x=$\frac{1}{2}$×1×2,
解得x=$\frac{2}{3}$,
∴PM=$\frac{2}{3}$,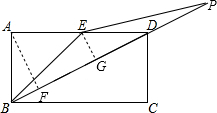 ∴BP=$\frac{PM}{sin∠ABD}$=$\frac{\frac{2}{3}}{\frac{2}{\sqrt{5}}}$=$\frac{\sqrt{5}}{3}$;
∴BP=$\frac{PM}{sin∠ABD}$=$\frac{\frac{2}{3}}{\frac{2}{\sqrt{5}}}$=$\frac{\sqrt{5}}{3}$;
③当EB=EP时,如图,过A作AF⊥BD于F,过E作EG⊥BD于G.
在Rt△ABF中,AF=AB•sin∠ABF=1×$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∵AE=ED,EG∥AF,
∴EG=$\frac{1}{2}$AF=$\frac{\sqrt{5}}{5}$.
在Rt△BEG中,∵BE=$\sqrt{2}$,EG=$\frac{\sqrt{5}}{5}$,
∴BG=$\sqrt{B{E}^{2}-E{G}^{2}}$=$\frac{3\sqrt{5}}{5}$.
∵EB=EP,EG⊥BP,
∴BP=2BG=$\frac{6\sqrt{5}}{5}$.
综上所述,线段BP的长度等于$\sqrt{2}$或$\frac{\sqrt{5}}{3}$或$\frac{6\sqrt{5}}{5}$.
故答案为$\sqrt{2}$或$\frac{\sqrt{5}}{3}$或$\frac{6\sqrt{5}}{5}$.
点评 本题考查了勾股定理的应用,矩形的性质,等腰直角三角形的判定与性质,等腰三角形的性质,锐角三角函数的定义等知识,综合性较强,有一定难度.进行分类讨论与数形结合是解题的关键.


科目:初中数学 来源: 题型:填空题
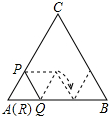 如图,正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为2π cm.(结果保留π)
如图,正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为2π cm.(结果保留π)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com