
分析 (1)将m=2代入原方程,公式法求得方程的解;
(2)根据方程有两个相等实数根可得△=0,列出关于m的方程,解方程可得;
(3)将分式化简,再将m的值代入计算即可.
解答 解:(1)当m=2时,一元二次方程为:3x2-6x+2=0,
解得:x=$\frac{6±\sqrt{(-6)^{2}-4×3×2}}{2×3}$=$\frac{3±\sqrt{3}}{3}$,
故方程的解为:x1=$\frac{3+\sqrt{3}}{3}$,x2=$\frac{3-\sqrt{3}}{3}$;
(2)∵一元二次方程3x2-6x+m=0有两个相等的实数根,
∴判别式△=(-6)2-4×3×m=0,
解得:m=3,
故m=3时,一元二次方程3x2-6x+m=0有两个相等的实数根;
(3)($\frac{{m}^{2}}{m+1}+4$)$÷\frac{{m}^{2}-4}{m+1}$=($\frac{{m}^{2}}{m+1}+\frac{4m+4}{m+1}$)÷$\frac{(m+2)(m-2)}{m+1}$
=$\frac{(m+2)^{2}}{m+1}$×$\frac{m+1}{(m+2)(m-2)}$
=$\frac{m+2}{m-2}$,
当m=3时,原分式=$\frac{3+2}{3-2}$=5.
点评 本题主要考查解一元二次方程、根的判别式、分式化简求值,根据方程的根的判别式得出相应方程是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | x•(32-2x+1)=130 | B. | $\frac{{({32-2x+1})}}{2}•x=130$ | C. | x•(32-2x-1)=130 | D. | $\frac{{({32-2x-1})}}{2}•x=130$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
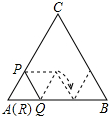 如图,正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为2π cm.(结果保留π)
如图,正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为2π cm.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
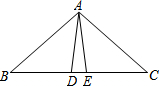 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )| A. | △ABE≌△ACD | B. | △ABD≌△ACE | C. | ∠C=30° | D. | ∠DAE=40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
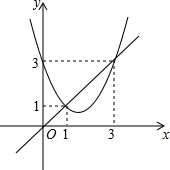 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com