
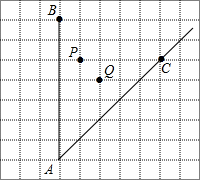
 如图,在边长为1个单位长度的小正方形组成的网格中,请分别在边AB,AC上找到点E,F,使四边形PEFQ的周长最小.
如图,在边长为1个单位长度的小正方形组成的网格中,请分别在边AB,AC上找到点E,F,使四边形PEFQ的周长最小.  高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a+m | B. | $\frac{ma}{m+n}$ | C. | $\frac{a}{m+n}$ | D. | $\frac{m+n}{am}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两枚骰子的点数的和可能为11 | B. | 两枚骰子的点数不可能相同 | ||
| C. | 两枚骰子的点数一定相同 | D. | 两枚骰子的点数的差可能为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,P为正方形ABCD内一点,且PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′.若BP的长为整数,则AP=$\sqrt{7}$或1.
如图,P为正方形ABCD内一点,且PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′.若BP的长为整数,则AP=$\sqrt{7}$或1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由.
已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com