
 已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由.
已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由. 分析 求出两个正方形的边长,根据面积大的比较合理来选择.
解答 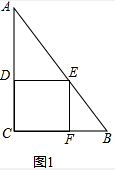 解:图1中,设DE=CD=EF=CF=x,
解:图1中,设DE=CD=EF=CF=x,
∵DE∥BC,
∴$\frac{DE}{BC}=\frac{AD}{AC}$,
∴$\frac{x}{6}=\frac{8-x}{8}$,
∴x=$\frac{24}{7}$,
图2中,作CM⊥AB垂足为M交DE于N.设正方形DEFG边长为y.
在RT△ABC中,∵AC=8,BC=6,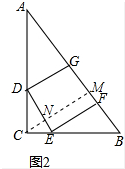 ∴AB=$\sqrt{C{A}^{2}+B{C}^{2}}$=10,CM=$\frac{AC•BC}{AB}$=4.8,
∴AB=$\sqrt{C{A}^{2}+B{C}^{2}}$=10,CM=$\frac{AC•BC}{AB}$=4.8,
∵DE∥AB,
∴△CDE∽△CBA,
∴$\frac{DE}{AB}=\frac{CN}{CM}$,
∴$\frac{y}{10}=\frac{4.8-y}{4.8}$,
∴y=$\frac{120}{37}$.
∵x>y,
∴图1中正方形面积大,
故图1的剪法较为合理.
点评 本题考查相似三角形的应用、平行线分线段成比例定理、正方形的面积等知识,解题的关键是根据相似三角形的性质列出方程解决问题,学会转化的思想思考问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
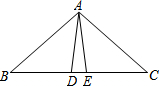 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )| A. | △ABE≌△ACD | B. | △ABD≌△ACE | C. | ∠C=30° | D. | ∠DAE=40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
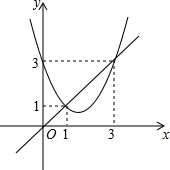 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这种抽查方式是普查 | B. | 1000名员工是总体 | ||
| C. | 每名员工的年薪是个体 | D. | 100名员工是总体的一个样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
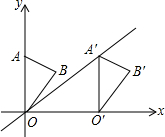 如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△0′A′B′,A的对应点A′是直线y=$\frac{4}{5}$x上一点,则点B与其对应点B′间的距离为( )
如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△0′A′B′,A的对应点A′是直线y=$\frac{4}{5}$x上一点,则点B与其对应点B′间的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com