
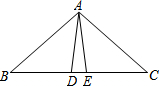
 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )| A. | △ABE≌△ACD | B. | △ABD≌△ACE | C. | ∠C=30° | D. | ∠DAE=40° |
分析 此题需要结合已知条件与相关知识用排除法来对第一结论进行验证从而确定最终答案.
解答 解:A、正确,
∵AD=AE,
∴∠ADE=∠AED,
∵BD=CE,
∴BD+DE=CE+DE,即BE=CD,
∴△ABE≌△ACD(SAS),
B、正确,
∵△ABE≌△ACD,
∴AB=AC,∠B=∠C,
∵BD=CE,
∴△ABD≌△ACE(SAS),
C、正确,
∵∠BAE=70°,
∴∠BAD=50°,
∵∠ADB=∠AEC=100°
∴∠B=∠C=30°,
D、错误,
∵∠ADB=∠AEC=100°,
∴∠ADE=∠AED=80°,
∴∠DAE=20°,
故选D.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.做题时,要结合已知条件与全等的判定方法对选项逐一验证.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:填空题
 如图,P为正方形ABCD内一点,且PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′.若BP的长为整数,则AP=$\sqrt{7}$或1.
如图,P为正方形ABCD内一点,且PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′.若BP的长为整数,则AP=$\sqrt{7}$或1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由.
已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若x2=4,则x=2 | |
| B. | 方程x2=x的解为x=1 | |
| C. | 若x2+2x+k=0有一根为2,则k=-8 | |
| D. | 若分式$\frac{{{x^2}-3x+2}}{x-1}$值为零,则x=1,2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com