
分析 (1)由于抛物线与x轴有两个不同的交点,所以b2-4ac>0;套用材料中的公式可求得线段AB的表达式,利用公式法可得到顶点C的纵坐标,进而求得斜边AB上的高(设为CD),若△ABC为等腰直角三角形,那么AB=2CD,可根据这个等量关系求出b2-4ac的值.
(2)方法同(1),只不过AB、CD的等量关系为:$\sqrt{3}$AB=2CD.
(3)若要改变∠ACB的大小,就必须向上或向下平移抛物线;首先根据(1)题的结论求出k的值,然后设出平移后的抛物线解析式,进而套用(2)的结论求出平移的距离,由此确定平移方案.
解答 解:(1)当△ABC为等腰直角三角形时,过C作CD⊥AB于D,则AB=2CD;
∵抛物线与x轴有两个交点,
∴△>0,
∴|b2-4ac|=b2-4ac,
∵AB=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$,
∵CD=$\frac{1}{2}$AB,
又∵CD=$\frac{\sqrt{{b}^{2}-4ac}}{2|a|}$,a≠0,
∴$\sqrt{{b}^{2}-4ac}$=$\frac{{b}^{2}-4ac}{2}$,
即$\sqrt{{b}^{2}-4ac}$=$\sqrt{\frac{({b}^{2}-4ac)^{2}}{4}}$,
∴b2-4ac=$\frac{({b}^{2}-4ac)^{2}}{4}$,
∵b2-4ac≠0,
∴b2-4ac=4.
(2)当△ABC为等边三角形时,b2-4ac=12.(解法同(1).)
(3)∵∠ACB=90°,
∴b2-4ac=4,即k2-4=4,
∴k=±2$\sqrt{2}$;
因为向左或向右平移时∠ACB的度数不变,
所以只需将抛物线y=x2±2$\sqrt{2}$x+1向上或向下平移使∠ACB=60°,然后向左或向右平移任意个单位即可.
设向上或向下平移后的抛物线的解析式为:
y=x2±2$\sqrt{2}$x+1+m,
∵平移后∠ACB=60°,
∴b2-4ac=12,
∴m=-2,
∴抛物线y=x2+kx+1向下平移2个单位后,向左或向右平移任意个单位都能使∠ACB的度数由90°变为60°.
点评 此题主要考查了根与系数的关系,用公式法求抛物线顶点坐标的方法以及直角三角形、等腰直角三角形、等边三角形的性质,解决此题的关键是读懂题意,弄清题目所给公式的含义.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:选择题
| A. | 当m=0时,x1=2,x2=3 | |
| B. | m>-$\frac{1}{4}$ | |
| C. | 当m>0时,2<x1<x2<3 | |
| D. | 二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
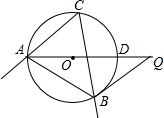 如图,⊙O是△ABC的外接圆,∠C=60°,AD是⊙O的直径,Q是AD延长线上的一点,且BQ=AB.
如图,⊙O是△ABC的外接圆,∠C=60°,AD是⊙O的直径,Q是AD延长线上的一点,且BQ=AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
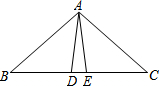 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )| A. | △ABE≌△ACD | B. | △ABD≌△ACE | C. | ∠C=30° | D. | ∠DAE=40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这种抽查方式是普查 | B. | 1000名员工是总体 | ||
| C. | 每名员工的年薪是个体 | D. | 100名员工是总体的一个样本 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com