
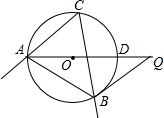
 如图,⊙O是△ABC的外接圆,∠C=60°,AD是⊙O的直径,Q是AD延长线上的一点,且BQ=AB.
如图,⊙O是△ABC的外接圆,∠C=60°,AD是⊙O的直径,Q是AD延长线上的一点,且BQ=AB.分析 (1)根据同弧所对的圆周等于圆心角的一半,结合等腰三角形的性质,可求∠OBQ=90°;
(2)①设出半径,表示出OQ,运用三角函数建立方程即可求解;
②过点C作CH⊥EF,垂足为H,交AB于点K,推理出“EF随着HK的增大而增大,当HK取最大值时,EF取最大值”即可求解.
解答 解:如图1,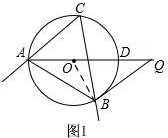
(1)连接OB,
∵∠C=60°,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵BQ=AB,
∴∠Q=∠OAB=30°,
∴∠ABQ=120°,
∴∠OBQ=90°,
∴BQ是⊙O的切线;
(2)①设圆的半径为r,则OQ=6-r,
由(1)知,∠Q=30°,∠OBQ=90°,
∴$\frac{OB}{OQ}$=sin30°=$\frac{1}{2}$
∴$\frac{r}{6-r}$=$\frac{1}{2}$,
解得:r=2;
②如图2,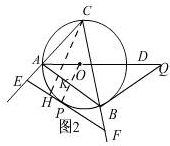
当OP垂直平分AB时,线段EF取得最大值;
理由如下:
由(1)知,AQ=6,∠Q=∠BAQ=30°,
可求AB=$2\sqrt{3}$,
过点C作CH⊥EF,垂足为H,交AB于点K,
∵EF∥AB,
∴CK⊥AB,△ABC∽△EFC,
∴$\frac{AB}{EF}=\frac{CK}{CH}$,
∴EF=$\frac{AB•CH}{CK}$=$2\sqrt{3}$×$\frac{CK+HK}{CK}$=$2\sqrt{3}$+$2\sqrt{3}$•$\frac{HK}{CK}$,
易知:CK是定值,所以,EF随着HK的增大而增大,
当HK取最大值时,EF取最大值,
∴当点P为劣弧AB的中点时,HK最大,此时OP垂直平分AB.
点评 此题主要考查圆的综合问题,会证明圆的切线,会运用方程思想解决问题,熟悉等腰三角形的性质并灵活运用,会结合相似三角形的性质进行推理是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
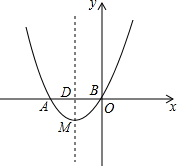 关于x的二次函数y=x2+(2n+1)x+n,它的图象为抛物线Cn,顶点为Mn.
关于x的二次函数y=x2+(2n+1)x+n,它的图象为抛物线Cn,顶点为Mn.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com