
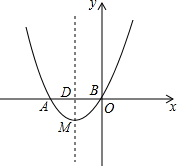
 关于x的二次函数y=x2+(2n+1)x+n,它的图象为抛物线Cn,顶点为Mn.
关于x的二次函数y=x2+(2n+1)x+n,它的图象为抛物线Cn,顶点为Mn.分析 (1)把抛物线解析式化为顶点式,即可求解;
(2)先根据题意确定n的值,求出点A,M,D的坐标,根据相似分类讨论即可求出符合条件的点P坐标;
(3)由题意分析,“与n的值无关”即解析式中n的系数为0,即可求解.
解答 解:(1)y=x2+(2n+1)x+n=$(x+\frac{2n+1}{2})^{2}$+$\frac{-4{n}^{2}-1}{4}$,
∴Mn($-\frac{2n+1}{2}$,$\frac{-4{n}^{2}-1}{4}$);
(2)如图1,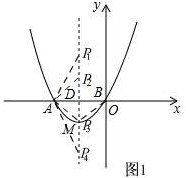
当n=0时,$\frac{-4{n}^{2}-1}{4}$的值最大,此时$\frac{-4{n}^{2}-1}{4}$=-$\frac{1}{4}$,
此时抛物线的解析式为:y=x2+x,
令y=0,解得:x=0,或x=-1,
∴点A(-1,0),B(0,0),
易求抛物线的对称轴l:x=$-\frac{1}{2}$,点M($-\frac{1}{2}$,-$\frac{1}{4}$),
此时,DM=$\frac{1}{4}$,DO=$\frac{1}{2}$,AD=$\frac{1}{2}$,
当△ADP与△MDO相似时,
$\frac{AD}{DM}=\frac{DP}{DO}$,
解得:DP=1,
此时,P2($-\frac{1}{2}$,1),P3($-\frac{1}{2}$,-1);
当△ADP与△ODM相似时,
$\frac{AD}{DO}=\frac{DP}{DM}$,
解得:DP=$\frac{1}{4}$,
此时,P1($-\frac{1}{2}$,$\frac{1}{4}$),P4($-\frac{1}{2}$,-$\frac{1}{4}$);
综上所述:满足条件的点P的坐标为:
P2($-\frac{1}{2}$,1),P3($-\frac{1}{2}$,-1),P1($-\frac{1}{2}$,$\frac{1}{4}$),P4($-\frac{1}{2}$,-$\frac{1}{4}$);
(3)由y=x2+(2n+1)x+n,
整理得:(2x+1)n+x2+x-y=0,
由题意,2x+1=0,且x2+x-y=0,
解得:x=$-\frac{1}{2}$,y=-$\frac{1}{4}$;
将x=$-\frac{1}{2}$,y=-$\frac{1}{4}$代入抛物线解析式恒成立,
所以符合条件的点T存在,其坐标为:T($-\frac{1}{2}$,-$\frac{1}{4}$).
点评 此题主要考查二次函数的综合问题,会把抛物线配方为顶点式,会根据相似三角形的性质分类解决点的存在性问题,知道抛物线恒过某一点的条件是解题的关键.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
| A. | m>-4 | B. | m>-3 | C. | m<-4 | D. | m<-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
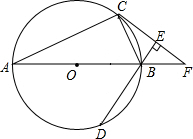 如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB,垂足为点E,直线AB与CE交于点F.
如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB,垂足为点E,直线AB与CE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
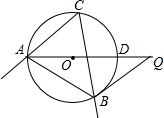 如图,⊙O是△ABC的外接圆,∠C=60°,AD是⊙O的直径,Q是AD延长线上的一点,且BQ=AB.
如图,⊙O是△ABC的外接圆,∠C=60°,AD是⊙O的直径,Q是AD延长线上的一点,且BQ=AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c与直线AB相交于A(-1,0)、B(2,3)两点,与y轴交于点C,其顶点为D.
如图,抛物线y=-x2+bx+c与直线AB相交于A(-1,0)、B(2,3)两点,与y轴交于点C,其顶点为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com