
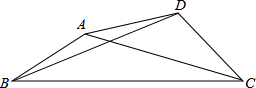
 如图,已知△ABC中,∠ABC=30°,AB=2,BC=3
如图,已知△ABC中,∠ABC=30°,AB=2,BC=3| 3 |
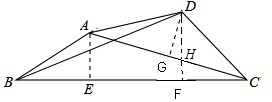 解:作AE⊥BC于E,
解:作AE⊥BC于E,| 3 |
| 3 |
| 13 |
| ||
| 2 |
| AG |
| cos∠DAC |
| ||||
|
| ||
| 3 |
| ||
| 6 |
| ||
| 3 |
| DG |
| EC |
| GH |
| AE |
| ||
| 12 |
| 5 |
| 12 |
| 13 |
| GH |
| DG |
| ||
| 6 |
| HF |
| FC |
| ||
| 6 |
| 3 |
| 3 |
| 5 |
| 12 |
| 3 |
| 5 |
| 36 |
| 3 |
| 5 |
| 6 |
| 3 |
| DC2-FC2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 6 |
| 3 |
| 13 |
| 6 |
| 3 |
| BF2+DF2 |
(
|
| 7 |
| 3 |
| 3 |


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
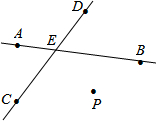 如图,直线CD与直线AB相交于E,根据下列语句画图.
如图,直线CD与直线AB相交于E,根据下列语句画图.查看答案和解析>>
科目:初中数学 来源: 题型:
 一个盒子里装有分别标有数字-2、-1、0、1、2、的五个光滑小球,这五个小球除标的数字外其余完全相同.现从该盒子中随机摸出一个小球其数字记为m,放回后再随机摸出一个小球其数字记为n.如图,在平面直角坐标系内,则点(m,n)恰好落在以点A(0,3)、B(2,0)、C(0,-2)、D(-2,0)为顶点的四形ABCD内部(不含边界)的概率是
一个盒子里装有分别标有数字-2、-1、0、1、2、的五个光滑小球,这五个小球除标的数字外其余完全相同.现从该盒子中随机摸出一个小球其数字记为m,放回后再随机摸出一个小球其数字记为n.如图,在平面直角坐标系内,则点(m,n)恰好落在以点A(0,3)、B(2,0)、C(0,-2)、D(-2,0)为顶点的四形ABCD内部(不含边界)的概率是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com