
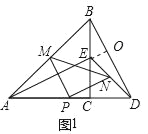
����Ŀ����ͼ1����ABC����CDE���ǵ���ֱ�������Σ�ֱ�DZ�AC��CD��ͬһ��ֱ���ϣ���M��N�ֱ���б��AB��DE���е㣬��PΪAD���е㣬����AE��BD��PM��PN��MN��
��1���۲���룺
ͼ1�У�PM��PN��������ϵ���� ����λ�ù�ϵ���� ����
��2��̽��֤����
��ͼ1�е���CDE���ŵ�C˳ʱ����ת����0�㣼����90�㣩���õ�ͼ2��AE��MP��BD�ֱ��ڵ�G��H���ж���PMN����״����˵�����ɣ�
��3����չ���죺
����CDE�Ƶ�C������ת����AC=4��CD=2����ֱ��д����PMN��������ֵ��

���𰸡���1��PM=PN��PM��PN��2����������3��![]()
��������
��1���ɵ���ֱ�������ε�������֤��ACE�ա�BCD���ɴ˿ɵ�AE=BD���ٸ�����������λ�߶������ɵõ�PM=PN����ƽ���ߵ����ʿɵ�PM��PN��
��2����1���еĽ����Ծɳ������ɣ�1���е�֤��˼·����֤����
��3���ɣ�2����֪��PMN�ǵ���ֱ�������Σ�PM=![]() BD���Ƴ���BD��ֵ���ʱ��PM��ֵ�����PMN���������Ƴ���B��C��D����ʱ��BD�����ֵ=BC+CD=6���ɴ˼��ɽ�����⣻
BD���Ƴ���BD��ֵ���ʱ��PM��ֵ�����PMN���������Ƴ���B��C��D����ʱ��BD�����ֵ=BC+CD=6���ɴ˼��ɽ�����⣻
��1��PM=PN��PM��PN���������£�
�ӳ�AE��BD��O��
�ߡ�ACB����ECD�ǵ���ֱ�������Σ�
��AC=BC��EC=CD����ACB=��ECD=90�㣮
����ACE����BCD��
 ��
��
���ACE�ա�BCD��SAS����
��AE=BD����EAC=��CBD��
�ߡ�EAC+��AEC=90�㣬��AEC=��BEO��
���CBD+��BEO=90�㣬
���BOE=90������AE��BD��
�ߵ�M��N�ֱ���б��AB��DE���е㣬��PΪAD���е㣬
��PM=![]() BD��PN=
BD��PN=![]() AE��
AE��
��PM=PM��
��PM��BD��PN��AE��AE��BD��
���NPD=��EAC����MPA=��BDC����EAC+��BDC=90�㣬
���MPA+��NPC=90�㣬
���MPN=90�㣬
��PM��PN��
�ʴ��ǣ�PM=PN��PM��PN��
��2����ͼ���У���AE��BC��O��
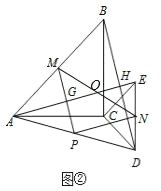
�ߡ�ACB����ECD�ǵ���ֱ�������Σ�
��AC=BC��EC=CD��
��ACB=��ECD=90�㣬
���ACB+��BCE=��ECD+��BCE��
���ACE=��BCD��
���ACE�ա�BCD��
��AE=BD����CAE=��CBD��
�֡ߡ�AOC=��BOE��
��CAE=��CBD��
���BHO=��ACO=90�㣬
�ߵ�P��M��N�ֱ�ΪAD��AB��DE���е㣬
��PM=![]() BD��PM��BD��
BD��PM��BD��
PN=![]() AE��PN��AE��
AE��PN��AE��
��PM=PN��
���MGE+��BHA=180�㣬
���MGE=90�㣬
���MPN=90�㣬
��PM��PN��
��3���ɣ�2����֪��PMN�ǵ���ֱ�������Σ�PM=![]() BD��
BD��
�൱BD��ֵ���ʱ��PM��ֵ�����PMN��������
�൱B��C��D����ʱ��BD�����ֵ=BC+CD=6��
��PM=PN=3��
���PMN����������ֵ=![]() ��3��3=
��3��3=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣��Գ���Ϊx=![]() ���Ҿ����㣨2��0����������˵������abc��0����a+b=0����4a+2b+c��0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ� ��
���Ҿ����㣨2��0����������˵������abc��0����a+b=0����4a+2b+c��0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ� ��

A���٢ڢ� B���ۢ� C���٢ۢ� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��![]() +bx+c��x���ڵ�A����2��0���͵�B����y���ڵ�C��0��3������D��x����һ���㣬����CD�����߶�CD�Ƶ�D��ת�õ�DE������E��ֱ��l��x�ᣬ����ΪH������C��CF��l��F������DF��
+bx+c��x���ڵ�A����2��0���͵�B����y���ڵ�C��0��3������D��x����һ���㣬����CD�����߶�CD�Ƶ�D��ת�õ�DE������E��ֱ��l��x�ᣬ����ΪH������C��CF��l��F������DF��
��1���������߽���ʽ��
��2�����߶�DE��CD�Ƶ�D˳ʱ����ת90���õ������߶�DF�ij���
��3�����߶�DE��CD�Ƶ�D��ת90���õ����ҵ�Eǡ�����������ϣ��������E�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ����������
����������![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() �ӳ����ϵ�һ�㣬
�ӳ����ϵ�һ�㣬![]() ��
��
![]() ��֤
��֤![]() ��
��

![]() �Ķ����в��ϣ�
�Ķ����в��ϣ�
��ͼ![]() ����
����![]() ��ֱ��
��ֱ��![]() ƽ���ƶ��߶�
ƽ���ƶ��߶�![]() �ij��ȣ����Ա䵽
�ij��ȣ����Ա䵽![]() ��λ�ã�
��λ�ã�

��ͼ![]() ����
����![]() ���
���![]() ����
����![]() �����Ա䵽
�����Ա䵽![]() ��λ�ã�
��λ�ã�

��ͼ![]() ���Ե�
���Ե�![]() Ϊ���İ�
Ϊ���İ�![]() ��ת
��ת![]() �����Ա䵽
�����Ա䵽![]() ��λ�ã�
��λ�ã�

������������һ��������������һ�������ΰ�ƽ���ƶ������ۡ���ת�ȷ�����ɵģ�����ֻ�ı�λ�ã����ı���״��С��ͼ�α任�����������ε�ȫ�ȱ任��
�ش��������⣺
����ͼ![]() �У�����ͨ��ƽ���ƶ������ۡ���ת�е���һ�ַ���ʹ
�У�����ͨ��ƽ���ƶ������ۡ���ת�е���һ�ַ���ʹ![]() �䵽
�䵽![]() ��λ�ã�
��λ�ã�
��________��
��ָ��ͼ![]() �У��߶�
�У��߶�![]() ��
��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��
��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У���D����B��90�㣬AEƽ�֡�DAB��CFƽ�֡�DCB.���жϡ�AEF���CFE�Ƿ���ȣ���֤����Ľ���.
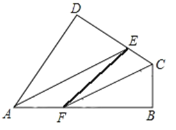
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
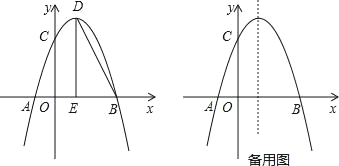
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ�ڵ�A�͵�B��3��0������y�ύ�ڵ�C��0��3������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������DB��
��1����������ߵĽ���ʽ������D�����ꣻ
��2����M���������ϵĶ��㣬���M�ĺ�����Ϊm��
������MBA=��BDEʱ�����M�����ꣻ
������M��MN��x�ᣬ�������߽��ڵ�N��PΪx����һ�㣬����PM��PN������PMN����MN���ۣ�����QMN�����ı���MPNQǡ��Ϊ�����Σ�ֱ��д��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ����������. �����ε����Ķ��壺���������ߵĴ�ֱƽ�����ཻ��һ�㣬�������������ε����ģ���ͼ1��ֱ��![]() �ֱ��DZ�
�ֱ��DZ�![]() �Ĵ�ֱƽ����.
�Ĵ�ֱƽ����.
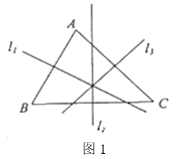
��֤��ֱ��![]() �ཻ��һ��.
�ཻ��һ��.
֤������ͼ2����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���ֱ�����
���ֱ�����![]()
��![]() ��
��![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() ��������1��
��������1��
��![]() ��
��![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() ��
��
��![]() ��������2��
��������2��
��![]() ��
��![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
���![]() ��
��![]() �ϣ�������3��
�ϣ�������3��
��ֱ��![]() �ཻ��һ��.
�ཻ��һ��.
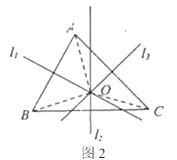
��1������֤�������е�������1��������2��������3���ֱ�ָʲô��
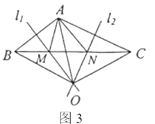
��2����ͼ3��ֱ��![]() �ֱ���
�ֱ���![]() �Ĵ�ֱƽ���ߣ�ֱ��
�Ĵ�ֱƽ���ߣ�ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() �����ģ�
�����ģ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ���ֱ�����
���ֱ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() . ��
. ��![]() ��
��![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����
����![]() ���ܳ�.
���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ���Զ�����豸��ˮ�ܣ���
���Զ�����豸��ˮ�ܣ���![]() �ڵ��棬��
�ڵ��棬��![]() �߳�����
�߳�����![]() �ף���
�ף���![]() ����һ�Զ���ת����ˮͷ����ÿһ˲�䣬�����ˮ����������״����ͷ
����һ�Զ���ת����ˮͷ����ÿһ˲�䣬�����ˮ����������״����ͷ![]() ��ˮ����ߵ�
��ˮ����ߵ�![]() ��������ˮƽ�߳�
��������ˮƽ�߳�![]() �ǣ�ˮ������ߵ�
�ǣ�ˮ������ߵ�![]() ����ͷ
����ͷ![]() �߳�
�߳�![]() �ף�����ͼ������ϵ�У�ˮ������ص�
�ף�����ͼ������ϵ�У�ˮ������ص�![]() ����
����![]() �ľ�����________�ף�
�ľ�����________�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��
��![]() �������������
�������������![]() ����
����![]() ����
����![]() ����
����![]() ����ȷ���ǣ� ��
����ȷ���ǣ� ��

A.�٢ڢ�B.�٢ڢ�C.�٢ۢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com