
����Ŀ���Ķ����в��ϣ����������. �����ε����Ķ��壺���������ߵĴ�ֱƽ�����ཻ��һ�㣬�������������ε����ģ���ͼ1��ֱ��![]() �ֱ��DZ�
�ֱ��DZ�![]() �Ĵ�ֱƽ����.
�Ĵ�ֱƽ����.
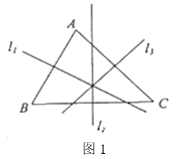
��֤��ֱ��![]() �ཻ��һ��.
�ཻ��һ��.
֤������ͼ2����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���ֱ�����
���ֱ�����![]()
��![]() ��
��![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() ��������1��
��������1��
��![]() ��
��![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
��![]() ��
��
��![]() ��������2��
��������2��
��![]() ��
��![]() �Ĵ�ֱƽ���ߣ�
�Ĵ�ֱƽ���ߣ�
���![]() ��
��![]() �ϣ�������3��
�ϣ�������3��
��ֱ��![]() �ཻ��һ��.
�ཻ��һ��.
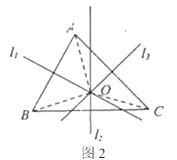
��1������֤�������е�������1��������2��������3���ֱ�ָʲô��
��2����ͼ3��ֱ��![]() �ֱ���
�ֱ���![]() �Ĵ�ֱƽ���ߣ�ֱ��
�Ĵ�ֱƽ���ߣ�ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() �����ģ�
�����ģ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ���ֱ�����
���ֱ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() . ��
. ��![]() ��
��![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����
����![]() ���ܳ�.
���ܳ�.
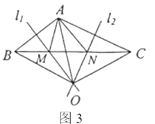
���𰸡���1������1���߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ�����ȣ�����2����������������3����һ���߶������˵������ȵĵ㣬�������߶εĴ�ֱƽ�����ϣ���2��![]()
��������
��1�������������̺ʹ�ֱƽ���ߵ����ʺ��ж��ó���
��2�����ݴ�ֱƽ���ߵ����ʵó�![]() ���ܳ�=BC��
���ܳ�=BC��![]() ���ٸ���
���ٸ���![]() ���ܳ����ɵó���
���ܳ����ɵó���
��1������1���߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ������
����2����������
����3����һ���߶������˵������ȵĵ㣬�������߶εĴ�ֱƽ������
��2���⣺��ֱ��![]() ��
��![]() �ĵĴ�ֱƽ����
�ĵĴ�ֱƽ����
��![]() ��
��
��ֱ��![]() ��
��![]() �ĵĴ�ֱƽ����
�ĵĴ�ֱƽ����
��![]()
��![]() ��
��![]() ���ܳ�
���ܳ�![]() ��
��
��![]() ���ܳ�Ϊ
���ܳ�Ϊ![]()
��![]() ��
��
��![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() .
.


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
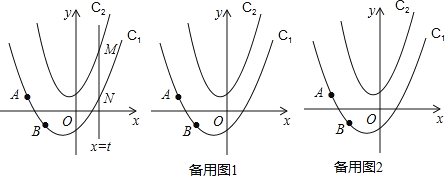
����Ŀ����ͼ����ƽ�������ϵ�У�������C1��y=ax2+bx��1������A����2��1���͵�B����1����1����������C2��y=2x2+x+1����ֱ��x=t��������C1���ڵ�N����������C2���ڵ�M��
��1����������C1�ı���ʽ��
��2��ֱ���ú�t�Ĵ���ʽ��ʾ�߶�MN�ij���
��3������AMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����t��ֵ��
��4���ڣ�3���������£���������C1��y�ύ�ڵ�P����M��y���Ҳ��������C2�ϣ�����AM��y���ڵ�k������KN����ƽ������һ��Q������KQ��QN����KQ=1�ҡ�KNQ=��BNPʱ����ֱ��д����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ͼ��ABCD�����������κ���y1=kx2+m��k��0����y2=ax2+b��a��0���IJ���ͼ��Χ�ɵķ��ͼ�Σ���֪A��1��0����B��0��1����D��0����3����

��1��ֱ��д�����������κ����ı���ʽ��
��2���ж�ͼ��ABCD�Ƿ�����ڽ������Σ������ε��ĸ�������ͼ��ABCD�ϣ�����˵�����ɣ�
��3����ͼ2������BC��CD��AD��������ƽ���ڣ���ʹ����BDC����ADE���ƣ����е�C���E�Ƕ�Ӧ���㣩�ĵ�E������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC����CDE���ǵ���ֱ�������Σ�ֱ�DZ�AC��CD��ͬһ��ֱ���ϣ���M��N�ֱ���б��AB��DE���е㣬��PΪAD���е㣬����AE��BD��PM��PN��MN��
��1���۲���룺
ͼ1�У�PM��PN��������ϵ���� ����λ�ù�ϵ���� ����
��2��̽��֤����
��ͼ1�е���CDE���ŵ�C˳ʱ����ת����0�㣼����90�㣩���õ�ͼ2��AE��MP��BD�ֱ��ڵ�G��H���ж���PMN����״����˵�����ɣ�
��3����չ���죺
����CDE�Ƶ�C������ת����AC=4��CD=2����ֱ��д����PMN��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ƴ��������������ƣ�ÿ����ȡ����y��Ԫ��������ʱ��x��Сʱ���ĺ�����ϵ��ͼ��ʾ������BA���߶Σ���BA��x�ᣬAC�����ߣ�
��1����x��30����y��x֮��ĺ�����ϵʽ��
��2����С��4�·�����20Сʱ����Ӧ������Ԫ���������ã�
��3����С��5�·���������Ϊ75Ԫ�������ڸ��·ݵ�����ʱ���Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������8�֣�ij�̼�Ԥ��һ��Ӧ�������ܳ����г�������13200Ԫ������һ�����ֳ��������к��Ȼ����Ӧ���̼�����28800Ԫ�����˵ڶ������ֳ��������������ǵ�һ����������2���������۹���10Ԫ��
��1�����̼ҹ����ĵ�һ�������Ƕ��ټ���
��2����������������ͬ�ı�����ۣ����ʣ��50���������Ż������������������ȫ������������ʲ�����25%���������������أ�����ôÿ�������ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �ֱ���˫����
�ֱ���˫����![]() �ڵ�һ���������ϵĵ㣬
�ڵ�һ���������ϵĵ㣬![]() �ᣬ
�ᣬ![]() �ᣬ����ֱ�Ϊ
�ᣬ����ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��Ľ��㣮��
��Ľ��㣮��![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() �����У� ��
������ ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B=32�㣬����ABC��ֱ��m���ۣ���B���ڵ�D��λ�ã����1-��2�Ķ����ǣ� ��
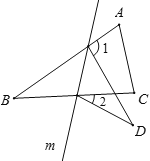
A. 32�� B. 64�� C. 65�� D. 70��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com