
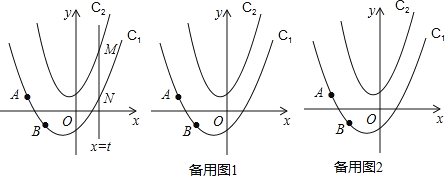
【题目】如图,在平面角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表示线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值;
(4)在(3)的条件下,设抛物线C1与y轴交于点P,点M在y轴右侧的抛物线C2上,连接AM交y轴于点k,连接KN,在平面内有一点Q,连接KQ和QN,当KQ=1且∠KNQ=∠BNP时,请直接写出点Q的坐标.
【答案】(1)抛物线C1:解析式为y=x2+x﹣1;(2)MN=t2+2;(3)t的值为1或0;(4)满足条件的Q点坐标为:(0,2)、(﹣1,3)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() )
)
【解析】(1)利用待定系数法进行求解即可;
(2)把x=t代入函数关系式相减即可得;
(3)根据图形分别讨论∠ANM=90°、∠AMN=90°时的情况即可得;
(4)根据题意画出满足条件图形,可以找到AN为△KNP对称轴,由对称性找到第一个满足条件Q,再通过延长和圆的对称性找到剩余三个点,利用勾股定理进行计算.
(1)∵抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),
∴![]() ,解得:
,解得:![]() ,
,
∴抛物线C1:解析式为y=x2+x﹣1;
(2)∵动直线x=t与抛物线C1交于点N,与抛物线C2交于点M,
∴点N的纵坐标为t2+t﹣1,点M的纵坐标为2t2+t+1,
∴MN=(2t2+t+1)﹣(t2+t﹣1)=t2+2;
(3)共分两种情况
①当∠ANM=90°,AN=MN时,由已知N(t,t2+t﹣1),A(﹣2,1),
∴AN=t﹣(﹣2)=t+2,
∵MN=t2+2,
∴t2+2=t+2,
∴t1=0(舍去),t2=1,
∴t=1;
②当∠AMN=90°,AN=MN时,由已知M(t,2t2+t+1),A(﹣2,1),
∴AM=t﹣(﹣2)=t+2,
∵MN=t2+2,
∴t2+2=t+2,
∴t1=0,t2=1(舍去),
∴t=0,
故t的值为1或0;
(4)由(3)可知t=1时M位于y轴右侧,根据题意画出示意图如图:
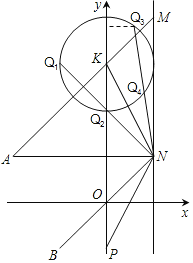
易得K(0,3),B、O、N三点共线,
∵A(﹣2,1),N(1,1),P(0,﹣1),
∴点K、P关于直线AN对称,
设⊙K与y轴下方交点为Q2,则其坐标为(0,2),
∴Q2与点O关于直线AN对称,
∴Q2是满足条件∠KNQ=∠BNP,
则NQ2延长线与⊙K交点Q1,Q1、Q2关于KN的对称点Q3、Q4也满足∠KNQ=∠BNP,
由图形易得Q1(﹣1,3),
设点Q3坐标为(a,b),由对称性可知Q3N=NQ1=BN=2![]() ,
,
由∵⊙K半径为1,
∴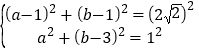 ,解得:
,解得: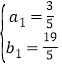 ,
,![]() ,
,
同理,设点Q4坐标为(a,b),由对称性可知Q4N=NQ2=NO=![]() ,
,
∴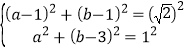 ,解得:
,解得: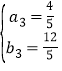 ,
,![]() ,
,
∴满足条件的Q点坐标为:(0,2)、(﹣1,3)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
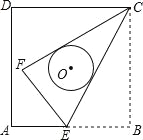
【题目】如图,正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )

A.①②④ B.③④ C.①③④ D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场香蕉的价格如下表
购买香蕉数(千克) | 不超过20千克 | 20千克以上但不超过40千克 | 40千克以上 |
每千克的价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克,已知第二次购买的数量多于第一次购买的数量,共付出264元,请问张强第一次,第二次分别购买香蕉多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以![]() 米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为
米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为![]() (米)与时间
(米)与时间![]() (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:

(1)填空:![]() ______;
______;![]() ______;
______;![]() ______.
______.
(2)求线段![]() 所在直线的解析式.
所在直线的解析式.
(3)若小军的速度是120米/分,求小军第二次与爸爸相遇时距图书馆的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成任务. 三角形的外心定义:三角形三边的垂直平分线相交于一点,这个点叫做三角形的外心,如图1,直线![]() 分别是边
分别是边![]() 的垂直平分线.
的垂直平分线.
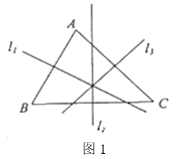
求证:直线![]() 相交于一点.
相交于一点.
证明:如图2,设![]() 相交于点
相交于点![]() ,分别连接
,分别连接![]()
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() ,(依据1)
,(依据1)
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() ,
,
∴![]() ,(依据2)
,(依据2)
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴点![]() 在
在![]() 上,(依据3)
上,(依据3)
∴直线![]() 相交于一点.
相交于一点.
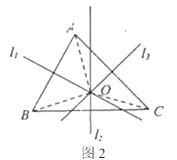
(1)上述证明过程中的“依据1”“依据2”“依据3”分别指什么?
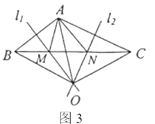
(2)如图3,直线![]() 分别是
分别是![]() 的垂直平分线,直线
的垂直平分线,直线![]() 相交于点
相交于点![]() ,点
,点![]() 是
是![]() 的外心,
的外心,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,分别连接
,分别连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() . 若
. 若![]() ,
,![]() 的周长为
的周长为![]() ,求
,求![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com