【题目】如图，
，
分别是双曲线
在第一、三象限上的点，
轴，
轴，垂足分别为
，
，点
是
与
轴的交点．设
的面积为
，
的面积为
，
的面积为
，则有（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
根据题意可以证明△DBA和△DQP相似，从而可以求出S1，S2，S3的关系.
解：延长QB与PA的延长线交于点D，如图所示，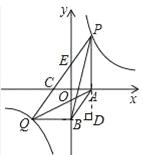
设点P的坐标为（a，b），点Q的坐标为（c，d），
∴DB=a，DQ=a﹣c，DA=﹣d，DP=b﹣d，
∵DBDP=a（b﹣d）=ab﹣ad=k﹣ad，
DADQ=﹣d（a﹣c）=﹣ad+cd=﹣ad+k=k﹣ad，
∴DBDP=DADQ，
即
，
∵∠ADB=∠PDQ，
∴△DBA∽△DQP，
∴AB∥PQ，
∴点B到PQ的距离等于点A到PQ的距离，
∴△PAB的面积等于△QAB的面积，
∵AB∥QC，AC∥BQ，
∴四边形ABQC是平行四边形，
∴AC=BQ，
∴△QAB的面积等于△QAC，
∴S1=S2=S3.
故选：D．
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=﹣
+bx+c交x轴于点A（﹣2，0）和点B，交y轴于点C（0，3），点D是x轴上一动点，连接CD，将线段CD绕点D旋转得到DE，过点E作直线l⊥x轴，垂足为H，过点C作CF⊥l于F，连接DF．
（1）求抛物线解析式；
（2）若线段DE是CD绕点D顺时针旋转90°得到，求线段DF的长；
（3）若线段DE是CD绕点D旋转90°得到，且点E恰好在抛物线上，请求出点E的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并完成任务. 三角形的外心定义：三角形三边的垂直平分线相交于一点，这个点叫做三角形的外心，如图1，直线
分别是边
的垂直平分线.
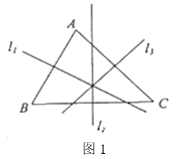
求证：直线相交于一点.
证明：如图2，设
相交于点
，分别连接
∵
是
的垂直平分线，
∴
，（依据1）
∵
是
的垂直平分线，
∴
，
∴
，（依据2）
∵
是
的垂直平分线，
∴点在上，（依据3）
∴直线相交于一点.
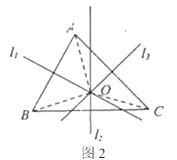
（1）上述证明过程中的“依据1”“依据2”“依据3”分别指什么？
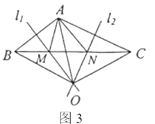
（2）如图3，直线分别是
的垂直平分线，直线相交于点，点 是
的外心，交于点
，交于点，分别连接
、
、
、
、
. 若
，
的周长为
，求
的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
是自动喷灌设备的水管，点
在地面，点
高出地面
米．在处有一自动旋转的喷水头，在每一瞬间，喷出的水流呈抛物线状，喷头与水流最高点
的连线与水平线成
角，水流的最高点与喷头高出
米，在如图的坐标系中，水流的落地点
到点的距离是________米．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长为100米．
（1）已知a=20，矩形菜园的一边靠墙，另三边一共用了100米木栏，且围成的矩形菜园面积为450平方米．如图1，求所利用旧墙AD的长；
（2）已知0＜α＜50，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩形菜园ABCD的面积最大，并求面积的最大值．
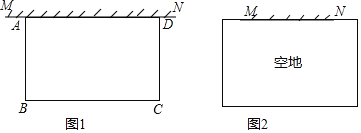
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两车从
地出发，沿同一条笔直的公路匀速驶向
地，乙车先到达地并停留
后，再以原速按原路返回，直至与甲车相遇.已知两车到地的距离
与甲车出发的时间
之间的函数关系分别如图中线段
和折线
所示，则图中点
的坐标为_______________.
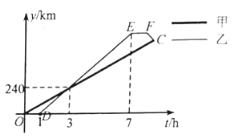
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某水果生产基地销售苹果，提供两种购买方式供客户选择
方式
：若客户缴纳
元会费加盟为生产基地合作单位，则苹果成交价为
元
千克.
方式
：若客户购买数量达到或超过
千克，则成交价为
元千克；若客户购买数量不足千克，则成交价为
元千克.设客户购买苹果数量为
（千克），所需费用为
（元）.
（1）若客户按方式购买，请写出（元）与（千克）之间的函数表达式;（备注：按方式购买苹果所需费用
生产基地合作单位会费
苹果成交总价）
（2）如果购买数量超过千克，请说明客户选择哪种购买方式更省钱;
（3）若客户甲采用方式购买，客户乙采用方式购买，甲、乙共购买苹果
千克，总费用共计
元，则客户甲购买了多少千克苹果？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
