
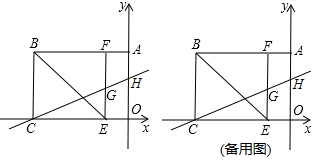
分析 (1)易知四边形BCEF是正方形,可得F(-1,3),G(-1,$\frac{3}{2}$),求出直线CG的解析式即可求出点H坐标;
(2)分两种情形①如图2中,当0<t≤4时.②如图3中,当4<t≤6时,分别求解即可;
(3)存在,如图④⑤⑥,点M就是直线MG和直线MN的交点,求解析式,再列方程组求解即可.
解答 解:(1)如图1中,易知四边形BCEF是正方形,BC=CE=BF=EF=3,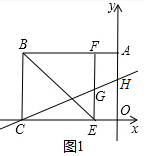
∵AB=OC=4,
∴AF=OE=1,
∴F(-1,3),G(-1,$\frac{3}{2}$),
∴直线CG的解析式为y=$\frac{1}{2}$x+2,
∴点H的坐标为(0,2),
故答案为(-1,3),(-1,$\frac{3}{2}$),H(0,2).
(2)①如图2中,当0<t≤4时,y=$\frac{1}{2}$•t•$\frac{3}{2}$=$\frac{3}{4}$t.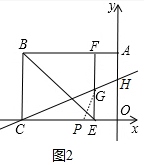
②如图3中,当4<t≤6时,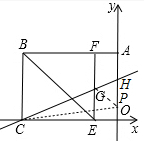
y=S△COH-S△COP-S△PGH=$\frac{1}{2}$×4×2-$\frac{1}{2}$×4×(t-4)-$\frac{1}{2}$×(6-t)×1=9-$\frac{3}{2}$t.
综上所述,y=$\left\{\begin{array}{l}{\frac{3}{4}x}&{(0<t≤4)}\\{9-\frac{3}{2}t}&{(4<t≤6)}\end{array}\right.$.
(3)存在,如图④,点N在y轴正半轴时,
设MG的解析式为:y=kx+b,
把C(-4,0),G(-1,1.5)代入得:
$\left\{\begin{array}{l}{-k+b=1.5}\\{-4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.5}\\{b=2}\end{array}\right.$,
∴MG:y=0.5x+2,
∴H(0,2),
∵四边形MNBG是平行四边形,
∴BN∥MG,
∴设BN的解析式为:y=0.5x+n,
把B(-4,3)代入得:n=5,
∴BN:y=0.5x+5,
∴N(0,5),
同理得BG:y=-0.5x+1,
∵MN∥BG,
∴MN:y=-0.5x+5,
则$\left\{\begin{array}{l}{y=-0.5x+5}\\{y=0.5x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=3}\\{y=3.5}\end{array}\right.$,
∴M(3,3.5).
如图⑤,点N在y轴负半轴时,
CG:y=0.5x+2,
∴设M(a,0.5a+2),
BG:y=-0.5x+1,则设MN:y=-0.5x+b,N(0,b),
∴3-(0.5a+2)=1.5-b,
-0.5a+b=0.5①,
把M(a,0.5a+2)代入MN中,0.5a+2=-0.5a+b,
a-b=-2②,
由①②得:a=-3,b=-1,
∴M(-3,0.5),
如图⑥,当BG为对角线时,G(-1,$\frac{3}{2}$),
∴EG=$\frac{3}{2}$,
过M作MP⊥BC于P,过G作GQ⊥y轴于Q,
易得△BMP≌△NGQ,
∴MP=GQ=1,
∵CE∥MP,
∴∠GCE=∠CMP,
∴tan∠GCE=tan∠CMP=$\frac{EG}{CE}$=$\frac{\frac{3}{2}}{3}$=$\frac{1}{2}$,
∴CP=$\frac{1}{2}$,
∴M(-5,-$\frac{1}{2}$),
综上所述:符合条件的点M的坐标为(3,3.5)、(-3,0.5)、(-5,-$\frac{1}{2}$).
点评 本题是四边形的综合题,综合考查出矩形、平行四边形、等腰直角三角形折叠的性质,与点的坐标和一次函数相结合,同时又运用了三角形的面积和解一元二次方程,知识点较多;运用了数形结合和分类讨论的思想,使问题得以解决,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
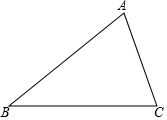 尺规作图:如图,已知△ABC,求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.(作图要求:写已知、求作,不写作法,保留作图痕迹)
尺规作图:如图,已知△ABC,求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.(作图要求:写已知、求作,不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
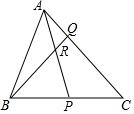 图中,AQC及BPC均为直线,AP为△ABC的一条角平分线,而BQ为△ABC的一条顶垂线,AP与BQ相交于R.若∠ABC=64°及∠ACB=46°,求∠PRQ.
图中,AQC及BPC均为直线,AP为△ABC的一条角平分线,而BQ为△ABC的一条顶垂线,AP与BQ相交于R.若∠ABC=64°及∠ACB=46°,求∠PRQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com