
某中学以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
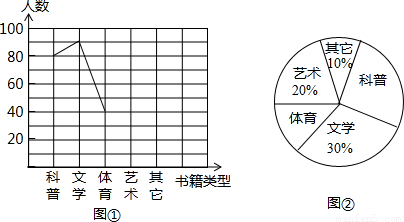
(1)300;(2)补图见解析;(3)48°;(4)480.
【解析】
试题分析:(1)用文学的人数除以所占的百分比计算即可得解.
(2)根据所占的百分比求出艺术和其它的人数,然后补全折线图即可.
(3)用体育所占的百分比乘以360°,计算即可得解.
(4)用总人数乘以科普所占的百分比,计算即可得解.
(1)∵90÷30%=300(名),
∴一共调查了300名学生.
(2)艺术的人数:300×20%=60名,其它的人数:300×10%=30名.
补全折线图如下:
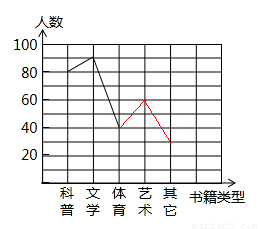
(3)体育部分所对应的圆心角的度数为: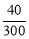 ×360°=48°.
×360°=48°.
(4)∵1800×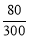 =480(名),
=480(名),
∴1800名学生中估计最喜爱科普类书籍的学生人数为480.
考点:1.折线统计图;2.扇形统计图;3.频数、频率和总量的关系;4.用样本估计总体.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:解答题
如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当点D′恰好落在EF边上时,求旋转角α的值;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;若不能说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:选择题
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6, 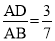 ,则EC的长是( )
,则EC的长是( )
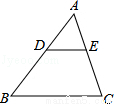
A.4.5 B.8 C.10.5 D.14
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,直线 分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线
分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线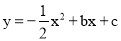 经过A,C两点,与
经过A,C两点,与 轴的另一交点为D.
轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线AB与CD的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,B,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:选择题
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:选择题
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为( )

A.70° B.80° C.40° D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com