
【题目】如图,射线![]() 平分
平分![]() ,
,![]() 为射线
为射线![]() 上一点,以
上一点,以![]() 为圆心,10为半径作
为圆心,10为半径作![]() ,分别与
,分别与![]() 两边相交于
两边相交于![]() 、
、![]() 和
和![]() 、
、![]() ,连结
,连结![]() ,此时有
,此时有![]() .
.
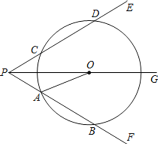
(1)求证:![]() ;
;
(2)若![]() ,求弦
,求弦![]() 的长;
的长;
【答案】(1)证明过程见解析;(2)12;
【解析】
(1)根据角平分线的定义可得∠DPO=∠BPO,然后根据平行线的性质可得∠DPO=∠POA,从而得出∠BPO=∠POA,然后根据等角对等边即可证出结论;
(2)过点O作OH⊥AB于点H,根据垂径定理可得![]() ,然后根据锐角三角函数证出PH=2OH,设OH=x,则PH=2x,根据勾股定理列出方程即可求出x,从而求出AH和AB.
,然后根据锐角三角函数证出PH=2OH,设OH=x,则PH=2x,根据勾股定理列出方程即可求出x,从而求出AH和AB.
(1)证明:∵PG平分∠EPF,
∴∠DPO=∠BPO,
∵OA∥PE,
∴∠DPO=∠POA,
∴∠BPO=∠POA,
∴PA=OA;
(2)解:过点O作OH⊥AB于点H,则![]()
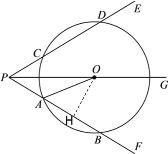
∵![]()
∴PH=2OH
设OH=x,则PH=2x,
由(1)可知PA=OA=10,
∴AH=PH-PA=2x-10,
∵AH2+OH2=OA2,
∴(2x-10)2+x2=102
解得x1=0(不合题意,舍去),x2=8,
∴AH=6,
∴AB=2AH=12;


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】小明在研究抛物线![]() (
(![]() 为常数)时,得到如下结论,其中正确的是( )
为常数)时,得到如下结论,其中正确的是( )
A.无论![]() 取何实数,
取何实数,![]() 的值都小于0
的值都小于0
B.该抛物线的顶点始终在直线![]() 上
上
C.当![]() 时,
时,![]() 随
随![]() 的增大而增大,则
的增大而增大,则![]()
D.该抛物线上有两点![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三台县教育和体育局为帮助万福村李大爷“精准脱贫”,在网上销售李大爷自己手工做的竹帘,其成本为每张40元,当售价为每张80元时,每月可销售100张.为了吸引更多顾客,采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5张.设每张竹帘的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 张.
张.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)李大爷深感扶贫政策给自己带来的好处,为了回报社会,他决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,求销售单价应该定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生参加“新冠肺炎”防疫知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题:
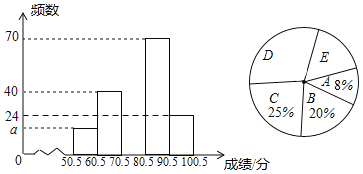
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中E小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC于点 D.
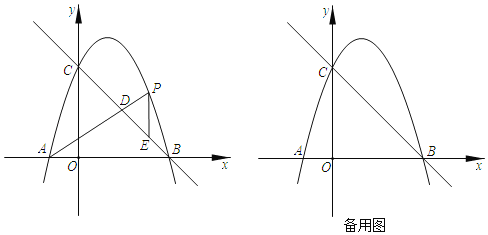
(1)求抛物线的函数表达式;
(2)当AD=2PD时,求点P的坐标;
(3)求线段![]() 的最大值;
的最大值;
(4)当线段![]() 最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.
最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
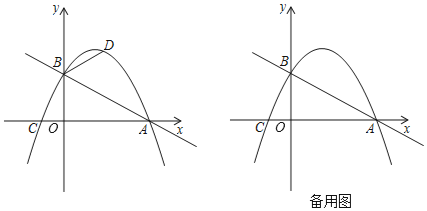
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点
与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与x轴的负半轴交于点
两点且与x轴的负半轴交于点![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 已知
已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当
和抛物线上的动点,当![]() 为顶点的四边形是平行四边形时,直接写出所有符合条件的
为顶点的四边形是平行四边形时,直接写出所有符合条件的![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
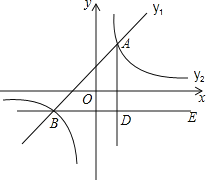
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
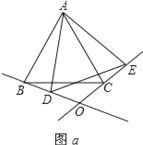
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.

(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com