
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
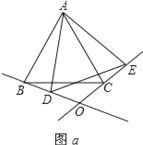
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .

【答案】(1)全等,理由见解析;(2)120°;(3)![]() .
.
【解析】
(1)结论:△ABD≌△ACE.根据SAS证明即可.
(2)利用全等三角形的性质解决问题即可.
(3)如图b中,AD交AE于J.设△ABC的外接圆的圆心为K.证明∠AOC=120°,推出点O的运动轨迹是K为圆心,KC半径的圆弧,圆心角为60°从而可以求得运动的轨迹.
解:(1)结论:△ABD≌△ACE.
∵△ADE是由△ABC绕点A旋转θ得到,∴△ABC是等边三角形.
∴AB=AD=AC=AE,∠BAD=∠CAE=20°,
在△ABD与△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).
(2)由已知得:△ABC和△ADE是全等的等边三角形,∴AB=AD=AC=AE.
∵△ADE是由△ABC绕点A旋转θ得到的,∴∠BAD=∠CAE=θ.
∴△BAD≌△CAE(SAS).∴∠ADB=∠AEC.
∵∠ADB+∠ABD+∠BAD=180°,∴∠AEC+∠ABO+∠BAD=180°.
∵∠ABO+∠AEC+∠BAE+∠BOE=360°,∠BAE=∠BAD+∠DAE,
∴∠DAE+∠BOE=180°.
又∵∠DAE=60°,∴∠BOE=120°.
(3)如图b中,AD交AE于J.设△ABC的外接圆的圆心为K.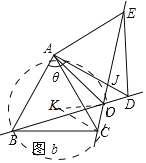
∵△ABD≌△ACE,
∴∠ODJ=∠AEJ,
∵∠AJE=∠OJD,
∴∠EAJ=∠JOD=60°,
∴∠AOC=120°,
∴点O的运动轨迹是K为圆心,KC半径的圆弧,圆心角为60°.
∴当θ从60°到120°的旋转过程中,运动的轨迹为![]() =
=![]() ,
,
故答案为:![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】某社区计划对面积为3600m2的区域进行绿化,经投标,由甲,乙两个工程队来完成,已知甲队4天能完成绿化的面积等于乙队8天完成绿化的面积,甲队3天能完成绿化的面积比乙队5天能完成绿化面积多50m2
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)若甲队每天化费用是1.2万元,乙队每天绿化费用为0.5万元,要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
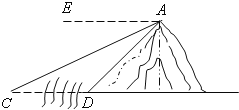
【题目】如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC是120米,求河宽CD的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
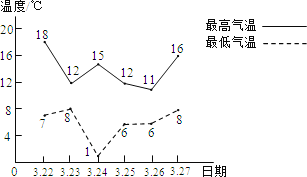
【题目】如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况.
(1)最低气温的中位数是 ℃;3月24日的温差是 ℃;
(2)分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;
(3)经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?
查看答案和解析>>
科目:初中数学 来源: 题型:
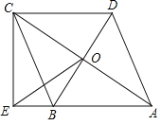
【题目】如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=2![]() ,BD=4,求OE的长.
,BD=4,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
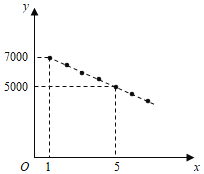
元,![]() 与
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
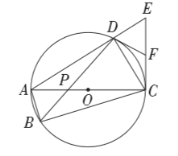
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了争创全国文明城市“六连冠”,写好2020年包头文明“答卷”,我市某班学生开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式对全年级同学进行卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,划分等级后的数据整理如下表:

同时该班又抽取了班里的8名学生(分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ),进行垃圾分类投放检测,检测结果如下表)其中“√”表示投放正确,“×”表示投放错误.
),进行垃圾分类投放检测,检测结果如下表)其中“√”表示投放正确,“×”表示投放错误.

根据上表回答问题:
(1)求本次问卷调查取样的样本容量和表中![]() 的值;
的值;
(2)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生;
(3)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生巾随机抽取2名进行访谈,请用列表或树状图法求抽到学生![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com