
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
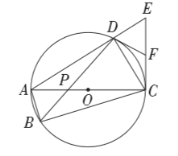
【答案】(1)见解析;(2)2;(3)4
【解析】
(1)连接OD,证明![]() ,由F为CE中点,得DF=CF,结合OD=OC,证明
,由F为CE中点,得DF=CF,结合OD=OC,证明![]() ,可得DF为
,可得DF为![]() 的切线;
的切线;
(2)证明△ACE∽△ADC,得AC2=AD·AE,可设DE=x(或DE=1),根据AC2=AD·AE求出AD,DC,![]() ,可得结果;
,可得结果;
(3)过点O作![]() 于点G,根据垂径定理得BG=GD=m,表示PD=m+PG,PB=m-PG,根据
于点G,根据垂径定理得BG=GD=m,表示PD=m+PG,PB=m-PG,根据![]() ,得
,得![]() ,由
,由![]() 得OG=PG,可得半径,即可得到AC.
得OG=PG,可得半径,即可得到AC.
解:(1)证明:如图,连接OD.
∵AC是⊙O的直径,
∴∠ADC=90°.
∴∠EDC=90°.
∵F是EC的中点,
∴DF=FC.
∴∠FDC=∠FCD.
∵OD=OC,
∴∠ODC=∠OCD.
∵AC⊥CE,
∴∠OCF=90°.
∴∠ODF=∠ODC+∠FDC=∠OCD+∠FCD=∠OCF=90°,即DF⊥OD.
∴DF是⊙O的切线.
(2)解:∵∠CAE+∠E=90°,∠CAE+∠ACD=90°,
∴∠E=∠ACD.
又∠ACE=∠ADC=90°,
∴△ACE∽△ADC.
∴![]() ,即AC2=AD·AE.
,即AC2=AD·AE.
解法一:设DE=x,则AC=![]() x,即(
x,即(![]() x)2=AD(AD+x).
x)2=AD(AD+x).
整理,得AD2+AD·x-20x2=0.
解得AD=4x或AD=-5x(舍去).
∴DC=![]() =2x.
=2x.
∴tan∠ABD=tan∠ACD=![]() =
=![]() =2.
=2.
解法二:设DE=1,则AC=![]() ,即(
,即(![]() )2=AD(AD+1).
)2=AD(AD+1).
整理,得AD2+AD-20=0.
解得AD=4或AD=-5(舍去).
∴DC=![]() =2.
=2.
∴tan∠ABD=tan∠ACD=![]() =2.
=2.
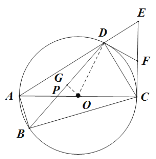
(3)解:如图,过点O作![]() 于点G.
于点G.
由垂径定理,得BG=DG.
设BG=DG=m,则PD=m+PG,PB=m-PG.
∵![]() ,
,
∴![]() ,整理,得
,整理,得![]() ,即
,即![]() .
.
∵∠DPC=45°,
∴OG=PG.
∴OD2=DG2+OG2=m2+PG2=4,即⊙O的半径为2.
∴AC=4.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某校组织学生参加“新冠肺炎”防疫知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题:
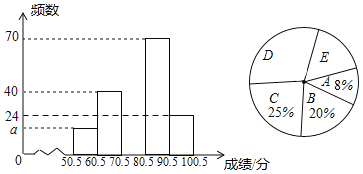
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中E小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
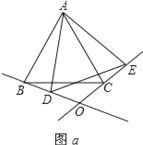
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为( )
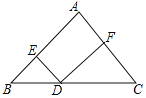
A. 34B. 32C. 22D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,过点
上的点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() .
.
(1)填空:点![]() _____________(填“在”或“不在”)
_____________(填“在”或“不在”)![]() 上;当
上;当![]() 时,
时,![]() 的值是_____________;
的值是_____________;
(2)如图1,在![]() 中,当
中,当![]() 时,求证:
时,求证:![]() ;
;
(3)如图2,当![]() 的顶点
的顶点![]() 是边
是边![]() 的中点时,请直接写出
的中点时,请直接写出![]() 三条线段的数量关系.
三条线段的数量关系.
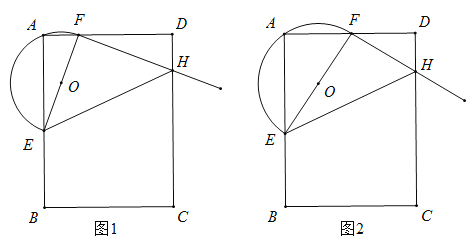
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.

(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们的东北方向距离12海里处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻艇以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻队出发到成功拦截捕鱼船所用的时间.
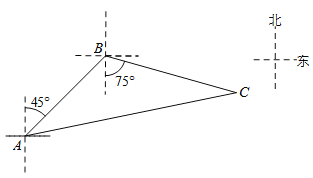
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABC是等腰直角三角形,∠B=90°,点B的坐标为(1,2).反比例函数![]() 的图象经过点C,一次函数y=ax+b的图象经A,C两点.
的图象经过点C,一次函数y=ax+b的图象经A,C两点.
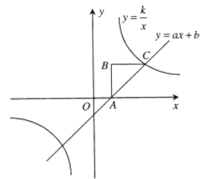
(1)求反比例函数和一次函数的关系式;
(2)直接写出不等式组0<ax+b≤![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com