
【题目】为了争创全国文明城市“六连冠”,写好2020年包头文明“答卷”,我市某班学生开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式对全年级同学进行卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,划分等级后的数据整理如下表:

同时该班又抽取了班里的8名学生(分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ),进行垃圾分类投放检测,检测结果如下表)其中“√”表示投放正确,“×”表示投放错误.
),进行垃圾分类投放检测,检测结果如下表)其中“√”表示投放正确,“×”表示投放错误.

根据上表回答问题:
(1)求本次问卷调查取样的样本容量和表中![]() 的值;
的值;
(2)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生;
(3)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生巾随机抽取2名进行访谈,请用列表或树状图法求抽到学生![]() 的概率.
的概率.
科目:初中数学 来源: 题型:
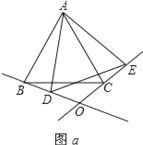
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.

(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
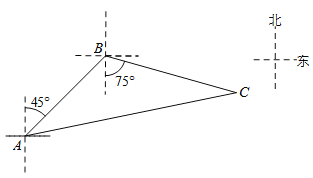
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们的东北方向距离12海里处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻艇以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻队出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:
的四个命题:
①当x=0时,y有最小值12;
②n为任意实数,x=3+n时的函数值大于x=3-n时的函数值;
③若n>3,且n是整数,当![]() 时,y的整数值有
时,y的整数值有![]() 个;
个;
④若函数图象过点![]() 和
和![]() ,其中a>0,b>0,则a<b.
,其中a>0,b>0,则a<b.
其中真命题的序号是( )
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .直线
.直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,设直线
是抛物线的顶点,设直线![]() 上方的抛物线上的动点
上方的抛物线上的动点![]() 的横坐标为
的横坐标为![]() .
.
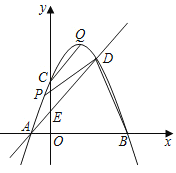
(1)连接![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)连接![]() ,
,![]() ,当
,当![]() 为何值时
为何值时![]() ?
?
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 为等腰直角三角形?若存在,请求出点
为等腰直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,这四张纸牌背面朝上洗匀.
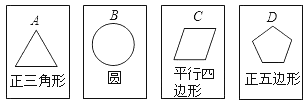
(1)从中随机摸出一张,求摸出的牌正面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则如下:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌正面图形都是轴对称图形,则小明获胜,否则小亮获胜,这个游戏公平吗?请用列表或画树状图的方法说明. (纸牌用![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABC是等腰直角三角形,∠B=90°,点B的坐标为(1,2).反比例函数![]() 的图象经过点C,一次函数y=ax+b的图象经A,C两点.
的图象经过点C,一次函数y=ax+b的图象经A,C两点.
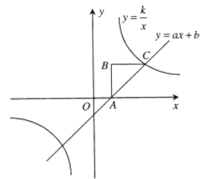
(1)求反比例函数和一次函数的关系式;
(2)直接写出不等式组0<ax+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D是边BC上一动点,连接AD,过点A作AE⊥AD,且AE=AD,连接CE.

(1)如图,求证:BD=CE;
(2)若AF平分∠DAE交直线BC于点F.
①如图,当点F在线段BC上,猜想线段BD,DF,FC之间的数量关系,并证明;
②若BD=6,CF=8,直接写出AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com