
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 边上一点,
边上一点,![]() ,点
,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 作直线分别与
作直线分别与![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() .若
.若![]() ,则
,则![]() 长为______
长为______![]() .
.
【答案】1或2
【解析】
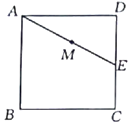
根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ=30°,再由PN与DC平行,得到∠PFA=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,再利用对称性确定出AP′的长即可.
根据题意画出图形,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() .
.

在![]() 中,
中,![]() ,
,![]() cm,
cm,
![]() cm.
cm.
根据勾股定理得![]() cm.
cm.
![]() 为
为![]() 的中点,
的中点,![]() cm,
cm,
在![]() 和
和![]() 中,
中,![]()
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
在![]() 中,
中,![]() ,
,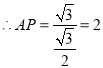 cm.
cm.
由对称性得到![]() cm,
cm,
综上,![]() 等于1cm或2cm.
等于1cm或2cm.
故答案为:1或2.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】在喜迎建党九十周年之际,某校举办校园唱红歌比赛,选出10名同学担任评委,并事先拟定从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分).
方案1:所有评委给分的平均分.
方案2:在所有评委中,去掉一个最高分和一个最低分,再计算剩余评委的平均分.
方案3:所有评委给分的中位数.
方案4:所有评委给分的众数.
为了探究上述方案的合理性,
先对某个同学的演唱成绩进行统计实验,右侧是这个同学的得分统计图:
(1)分别按上述四种方案计算这个同学演唱的最后得分.
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°.
(1)求A、B之间的路程;(参考数据: ![]() ,
, ![]() )
)
(2)请判断此校车是否超过了白田路每小时60千米的限制速度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
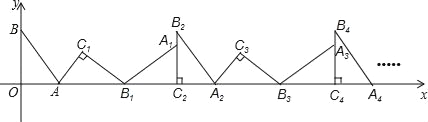
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
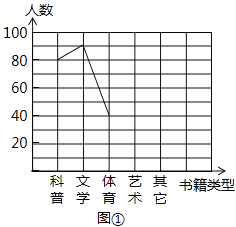
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF,若∠ABE=25°,则∠EFC'的度数为( )
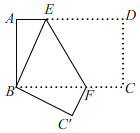
A.122.5°B.130°C.135°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.
(1)直接写出计算结果:2③= ,(-3)④ = ,![]() ⑤= .
⑤= .
(2)计算 24÷23 + (-8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
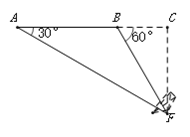
【题目】如图,在一次空中搜寻中,水平飞行的飞机观测到在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为60°的方向上,请你计算当飞机飞临F的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:![]() ≈1.7)
≈1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com