
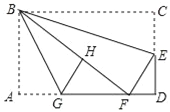
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG=![]() S△FGH.其中正确的是( )
S△FGH.其中正确的是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题分析:利用折叠性质得∠CBE=∠FBE,∠ABG=∠FBG,BF=BC=10,BH=BA=6,AG=GH,则可得到∠EBG=![]() ∠ABC,于是可对①进行判断;在Rt△ABF中利用勾股定理计算出AF=8,则DF=AD﹣AF=2,设AG=x,则GH=x,GF=8﹣x,HF=BF﹣BH=4,利用勾股定理得到x2+42=(8﹣x)2,解得x=3,所以AG=3,GF=5,于是可对②进行判断;接着证明△ABF∽△DFE,利用相似比得到
∠ABC,于是可对①进行判断;在Rt△ABF中利用勾股定理计算出AF=8,则DF=AD﹣AF=2,设AG=x,则GH=x,GF=8﹣x,HF=BF﹣BH=4,利用勾股定理得到x2+42=(8﹣x)2,解得x=3,所以AG=3,GF=5,于是可对②进行判断;接着证明△ABF∽△DFE,利用相似比得到![]() ,而
,而![]() ,所以
,所以![]() ,所以△DEF与△ABG不相似,于是可对③进行判断;分别计算S△ABG和S△GHF可对④进行判断.
,所以△DEF与△ABG不相似,于是可对③进行判断;分别计算S△ABG和S△GHF可对④进行判断.
解:∵△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,
将△ABG沿BG折叠,点A恰落在线段BF上的点H处,

∴∠CBE=∠FBE,∠ABG=∠FBG,BF=BC=10,BH=BA=6,AG=GH,
∴∠EBG=∠EBF+∠FBG=![]() ∠CBF+
∠CBF+![]() ∠ABF=
∠ABF=![]() ∠ABC=45°,所以①正确;
∠ABC=45°,所以①正确;
在Rt△ABF中,AF=![]() =8,
=8,
∴DF=AD﹣AF=10﹣8=2,
设AG=x,则GH=x,GF=8﹣x,HF=BF﹣BH=10﹣6=4,
在Rt△GFH中,∵GH2+HF2=GF2,
∴x2+42=(8﹣x)2,解得x=3,
∴GF=5,
∴AG+DF=FG=5,所以②正确;
∵△BCE沿BE折叠,点C恰落在边AD上的点F处
∴∠BFE=∠C=90°,
∴∠EFD+∠AFB=90°,
而∠AFB+∠ABF=90°,
∴∠ABF=∠EFD,
∴△ABF∽△DFE,
∴![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∴△DEF与△ABG不相似;所以③错误.
∵S△ABG=![]() ×6×3=9,S△GHF=
×6×3=9,S△GHF=![]() ×3×4=6,
×3×4=6,
∴S△ABG=1.5S△FGH.所以④正确.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 . 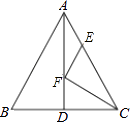
查看答案和解析>>
科目:初中数学 来源: 题型:
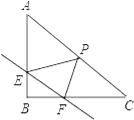
【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=![]() ,BC=
,BC=![]() .
.
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
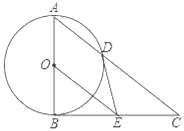
【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,若∠B=60°,点E、F分别在AB、AD上,且BE=AF,则∠AEC+∠AFC的度数等于( )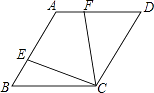
A.120°
B.140°
C.160°
D.180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com