
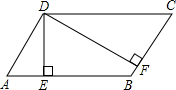
 如图,在平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若ABCD的周长为45,DE=5,DF=10,求平行四边形ABCD的面积.
如图,在平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若ABCD的周长为45,DE=5,DF=10,求平行四边形ABCD的面积.  轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
 在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )
在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )| A. | 两点之间线段最短 | B. | 两点确定一条直线 | ||
| C. | 垂线段最短 | D. | 过一点可以作无数条直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
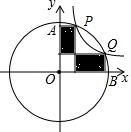 如图,点P(2,6)是函数y=$\frac{k}{x}$(k≠0)图象上的一点,以OP为半径作扇形OAB,交y轴于点A,交x轴于点B,且与函数y=$\frac{k}{x}$(k≠0)图象交于点Q.从点P,Q分别向x轴,y轴作垂线,则图中阴影部分的面积是16.
如图,点P(2,6)是函数y=$\frac{k}{x}$(k≠0)图象上的一点,以OP为半径作扇形OAB,交y轴于点A,交x轴于点B,且与函数y=$\frac{k}{x}$(k≠0)图象交于点Q.从点P,Q分别向x轴,y轴作垂线,则图中阴影部分的面积是16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,△A′B′C′是△ABC经过平移后得到的A(-4,-1),B(-5,-4),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
如图所示,△A′B′C′是△ABC经过平移后得到的A(-4,-1),B(-5,-4),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com