
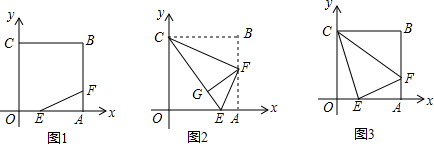
���� ��1�����ı���OABC�������Σ���B������Ϊ��4��4����OE=AF=1���õ���E��F�����꣬������⣻
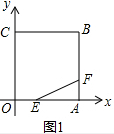
��2�����۵������ʵã�AE=GE��BF=GF=AF��CG=BC=4����ֱ��������COE�У��ɹ��ɶ����з������GE���������������Ƶõ���G�����ꣻ
��3����x���Ͻ�ȡOM=BF������CM������ȫ�������Σ����ݡ�ECF=45�㣬�õ���MCE=��MCO+��OCE=45�㣬�ֵõ�һ��ȫ�ȵ������Σ��õ��߶εĹ�ϵ��֤�á�AEF���ܳ�=8�Ǹ���ֵ�����ǵý⣮
���  �⣺��1����ͼ1���ı���OABC�������Σ���B������Ϊ��4��4����
�⣺��1����ͼ1���ı���OABC�������Σ���B������Ϊ��4��4����
��OA=AB=4��
��OE=AF=1��
��E��1��0����F��4��1����
��ֱ��EF�Ľ���ʽ��y=kx+b��
��$\left\{\begin{array}{l}{0=k+b}\\{1=4k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{1}{3}}\end{array}\right.$��
��ֱ��EF�Ľ���ʽ��y=$\frac{1}{3}x$+$\frac{1}{3}$��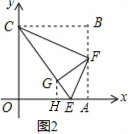
��2����ͼ2���۵������ʵã�AE=GE��BF=GF=AF��CG=BC=4��
��AE=GE=x����OE=4-x��CE=4+x��
�ࣨ4-x��2+42=��4+x��2��
��x=1����AE=GE=1��
����G��GH��OA��H��
��GH��OC����$\frac{GH}{OC}$=$\frac{EH}{OE}$=$\frac{EG}{EC}$=$\frac{1}{5}$��
��GH=$\frac{4}{5}$��EH=$\frac{3}{5}$��
��OH=$\frac{12}{5}$��
��G��$\frac{12}{5}$��$\frac{4}{5}$����
��3����ͼ3��x���Ͻ�ȡOM=BF������CM��
�ڡ�COM���BCF�У�
$\left\{\begin{array}{l}{OC=BC}\\{��MOC=��B}\\{OM=BF}\end{array}\right.$��
���OMC�ա�BFC��SAS����
��CM=CF����MCO=��FCB��
���MCF=FCE=45�㣬
�ڡ�MCE���FCE�У�
$\left\{\begin{array}{l}{CM=CF}\\{��MCE=��FCE}\\{CE=CE}\end{array}\right.$��
���MCE�ա�FCE��SAS����
��ME=EF��
��AEF���ܳ�=AF+EF+AE=ME+AE+AF=AE+OE+AF+BF=8��
��E��F���˶������У�������֡�ECF=45�㣬��AEF���ܳ����ᷢ���ı䣮
���� ���⿼���������ε����ʣ�ȫ�������ε��ж������ʣ����������ε��ж������ʣ�����ϵ������һ�κ����Ľ���ʽ��֪ʶ�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
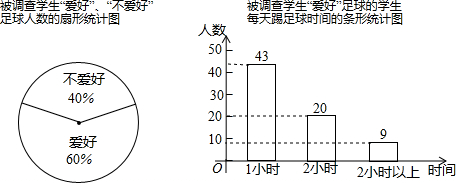
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
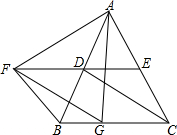 ��ͼ����G�ڱ�BC�ϣ���ABC�͡�AGF���ǵȱ������Σ���E�ڱ�AC�ϣ�FE��BC��EF��AB���ڵ�D��
��ͼ����G�ڱ�BC�ϣ���ABC�͡�AGF���ǵȱ������Σ���E�ڱ�AC�ϣ�FE��BC��EF��AB���ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
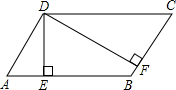 ��ͼ����ƽ���ı���ABCD�У�DE��AB��E��DF��BC��F����ABCD���ܳ�Ϊ45��DE=5��DF=10����ƽ���ı���ABCD�������
��ͼ����ƽ���ı���ABCD�У�DE��AB��E��DF��BC��F����ABCD���ܳ�Ϊ45��DE=5��DF=10����ƽ���ı���ABCD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
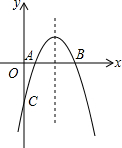 ��֪����ͼ��ʾ��������y=-x2+bx+c��x�����������ֱ�ΪA��1��0����B��3��0��
��֪����ͼ��ʾ��������y=-x2+bx+c��x�����������ֱ�ΪA��1��0����B��3��0���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com