
����Ŀ����ABC��һ�ŵ���ֱ��������ֽ�壬��C=90�㣬AC=BC=2�� 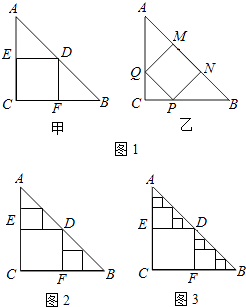
��1��Ҫ������ֽ���м���һ�������ܴ�������Σ��мס������ּ�������ͼ1�����Ƚϼס������ּ��������ּ������õ��������������˵�����ɣ�
��2��ͼ1�м��ּ�����Ϊ��1�μ�ȡ�����������������Ϊs1�����ռ��ּ����������µġ�ADE�͡�BDF�У��ֱ��ȡ�����Σ��õ�������ͬ�������Σ���Ϊ��2�μ�ȡ�����������������������Ϊs2����ͼ2������s2=���������µ��ĸ��������У���ͬ�������ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��3�μ�ȡ���������ĸ������������Ϊs3 �� ����������ȥ�������10�μ�ȡʱ��s10=��
��3�����10�μ�ȡ�����µ�����С�����ε����֮�ͣ�
���𰸡�
��1���⣺�ⷨ1����ͼ�ף������⣬��AE=DE=EC����EC=1��S������CFDE=12=1
��ͼ�ң���MN=x���������⣬��AM=MQ=PN=NB=MN=x��
�� ![]() ��
��
��� ![]()
�� ![]()
�֡� ![]()
����ּ������õ��������������
˵����ͼ������Ϊ��������õ�D��E��F�ֱ�ΪAB��AC��BC���е㣬S������OFDE=1��
�ⷨ2����ͼ�ף��������AE=DE=EC����EC=1��
��ͼ�ң���MN=x�����������AM=MQ=QP=PN=NB=MN=x��
�� ![]() ��
��
��� ![]() ��
��
�֡� ![]() ����EC��MN��
����EC��MN��
����ּ������õ��������������
��2���⣺ ![]() ��
��![]()
��3���⣺�ⷨ1��̽�����ɿ�֪�� ![]()
ʣ�������������Ϊ2����S1+S2+��+S10��=2����1+ ![]() +��+
+��+ ![]() ��=
��= ![]()
�ⷨ2���������֪��
��һ�μ�ȡ��ʣ�������������Ϊ2��S1=1=S1
�ڶ��μ�ȡ��ʣ�������������Ϊ ![]() ��
��
�����μ�ȡ��ʣ�������������Ϊ ![]() ��
��
��
��ʮ�μ�ȡ��ʣ�������������Ϊ ![]()
����������1���ֱ�����ס������ּ������õ���������������бȽϼ��ɣ���2����ͼ1�м��ּ�������֪��һ�������ε������ǰһ�������ε������ ![]() �����˿�֪�������3��̽�����ɿ�֪��
�����˿�֪�������3��̽�����ɿ�֪�� ![]() �����˹��ɿɵõ�10�μ�ȡ�����µ�����С�����ε����֮�ͣ�
�����˹��ɿɵõ�10�μ�ȡ�����µ�����С�����ε����֮�ͣ�
�����㾫�������յ���ֱ�������κ��ɶ����ĸ����ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ�ӡ���ԡ��ͷ���ܵ�����������һ����Ŀ�� �������Ͻ�ȡ��0��3�Ķ�Ӧ�߶�AB��ʵ��m��ӦAB�ϵĵ�M����ͼ1����AB�۳��������Σ�ʹ��A��B�غ��ڵ�P����ͼ2������ƽ��ֱ������ϵ��ƽ�ƴ������Σ�ʹ������y��Գƣ��ҵ�P������Ϊ��0��2����PM��x�ύ�ڵ�N��n��0������ͼ3����m= ![]() ʱ����n��ֵ��
ʱ����n��ֵ��
���������Ŀ�õ���nֵΪ�� ��
A.4��2 ![]()
B.2 ![]() ��4
��4
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ļ�����.
-4��![]() ��0��
��0��![]() ��-3.14��717��-��+5����+1.88��
��-3.14��717��-��+5����+1.88��![]()
��1���������ϣ��� �� ����
��2���������ϣ��� ������
��3���������ϣ��� ������
��4���������ϣ��� �� ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�����ͼ��ʾ��Rt��ABO��AB��x���ڵ�B��б��AO=10��sin��AOB= ![]() ������������
������������ ![]() ��ͼ��AO���е�C������AB���ڵ�D�����D������Ϊ ��
��ͼ��AO���е�C������AB���ڵ�D�����D������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����һ�����֣�
���⣺![]() �ܻ�Ϊ������ʽ��
�ܻ�Ϊ������ʽ��
̽�������![]() �������
�������![]() ��
��
�����![]() ,��
,��![]() ��
��
�����![]() ,��ã�
,��ã�![]() .
.
�������������ֵ����⣬�ش��������⣺
��1������ٵ�����ڵ�������ʲô��
��2����������̽����̣����㳢��![]() ��Ϊ������ʽ��
��Ϊ������ʽ��
��3�����㽫![]() ��Ϊ������ʽ����˵������.
��Ϊ������ʽ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AE����ABC�Ľ�ƽ���ߣ�AD��BC�ڵ�D����FΪBC���е㣬����BAC��104�㣬��C��40�����������н��ۣ��١�BAE��52�㣻�ڡ�DAE��2�㣻��EF��ED����S��ABF��![]() S��ABC.������ȷ�ĸ�����(����)
S��ABC.������ȷ�ĸ�����(����)
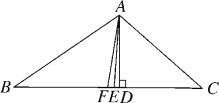
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O�ڵȱ���ABC�ڣ���AOB=100�㣬��BOC=x������BOC�Ƶ�C˳ʱ����ת60��������ADC������OD��
��1����COD����״���� ����
��2����x=150��ʱ����AOD����״���� ������ʱ��OB=3��OC=5����OA�ij���
��3����xΪ���ٶ�ʱ����AODΪ���������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ����1��13��![]() ��12��22����2��13+23��
��12��22����2��13+23��![]() ��22��32����3��13+23+33��
��22��32����3��13+23+33��![]() ��32��42����4��13+23+33+43��
��32��42����4��13+23+33+43��![]() ��42��52��
��42��52��![]()
����������ʽ�Ĺ��ɣ�����������⣺
��1��д����5����ʽ��_____��
��2��д����n����ʽ���ú���n�Ĵ���ʽ��ʾ����
��3����s����������s��2��Ӧ���㷢�ֵĹ��ɣ�����![]() ��s2����s+1��2��
��s2����s+1��2��![]() ����s��1��2��s2��
����s��1��2��s2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��������ı���չ��ͼ���������Ϸֱ����1��6�IJ�ͬ���֣��������۵��������壬���ཻ��ͬһ��������������ϵ�����֮�������� 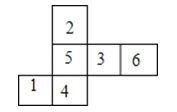
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com