
【题目】李老师从“淋浴龙头”受到启发.编了一个题目: 在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A,B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当m= ![]() 时,求n的值.
时,求n的值.
你解答这个题目得到的n值为( )
A.4﹣2 ![]()
B.2 ![]() ﹣4
﹣4
C.![]()
D.![]()
【答案】A
【解析】解:∵AB=3,△PDE是等边三角形, ∴PD=PE=DE=1,
以DE的垂直平分线为y轴建立直角坐标系,
∵△PDE关于y轴对称,
∴PF⊥DE,DF=EF,DE∥x轴,
∴PF= ![]() ,
,
∴△PFM∽△PON,
∵m= ![]() ,
,
∴FM= ![]() ﹣
﹣ ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得ON=4﹣2 ![]() .
.
故选:A.
【考点精析】本题主要考查了等边三角形的性质和轴对称的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】(12分)当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式:__________________________;
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图③中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)琪琪用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丁丁想在一个矩形材料中剪出如图阴影所示的梯形,作为要制作的风筝的一个翅膀.请你根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位, ![]() ≈1.7).
≈1.7). 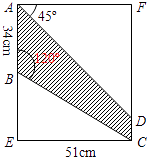
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O为数轴原点,点A表示的数是4,将线段OA沿数轴移动,移动后的线段记为O′A′.
(1)当点O′恰好是OA的中点时,数轴上点A′表示的数为 .
(2)设点A的移动距离AA′=x.
①当O′A=1时,求x的值;
②D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
![]()


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(2,1)、B(3,5)、C(5,-2)、D(0,1)、E(-1,5)、F(-3,-2),则△ABC与△DEF( )
A. 关于x轴对称 B. 关于直线x=1对称
C. 关于点(1,0)对称 D. 以上答案都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
① 求证:△ABE≌△CBD;
② 若∠CAE=30°,求∠BDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是一张等腰直角三角形纸板,∠C=90°,AC=BC=2, 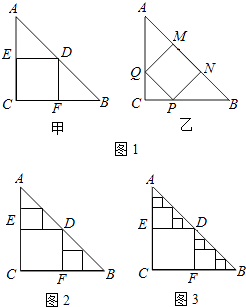
(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为s1;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2),则s2=;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为s3 , 继续操作下去…,则第10次剪取时,s10=;
(3)求第10次剪取后,余下的所有小三角形的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com